Absoluter Flächeninhalt - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Integrale
Absoluter Flächeninhalt einer Funktion:
Der Flächeninhalt eines Integrals wird unterhalb der x-Achse vom Flächeninhalt oberhalb der x-Achse abgezogen. Das ist durchaus vorteilhaft in der Ökonomie um beispielsweise Bestandsmengen zu errechnen. Dennoch ist es manchmal von Wichtigkeit, den absoluten Flächeninhalt des Intervalls zu ermitteln. Um dies zu tun, ist es zwangsweise erforderlich, das Intervall in Teilintervalle aufzuteilen, sofern innerhalb des Intervalls die x-Achse durch den Funktionsverlauf geschnitten wird und es sowohl eine Fläche oberhalb als auch unterhalb der x-Achse gibt. Eine Trennung des Intervalls muss genau am Schnittpunkt mit der x-Achse erfolgen.
Vorgehensweise zur Berechnung des absoluten Flächeninhalts eines Intervalls:
Schnittpunkte mit der x-Achse einer Funktion entsprechen den Nullstellen der Funktion. Es sind die Nullstellen der Funktion zu bestimmen und zu prüfen, ob diese innerhalb des Intervalls liegen. Liegen Nullstellen innerhalb des Intervalls, so ist das Intervall genau an dieser Stelle zu trennen. Die beiden Teilintervalle lauten dann, von der unteren Integrationsgrenze (𝑥_𝑎) bis zur Nullstelle (𝑥_0) und von der Nullstelle (𝑥_0) bis zur oberen Integrationsgrenze (𝑥_𝑏). Die beiden Teilintervalle sind dann zu errechnen und deren Ergebnisse als Beträge zu addieren. So erhält man den absoluten Flächeninhalt:
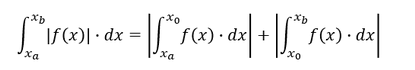
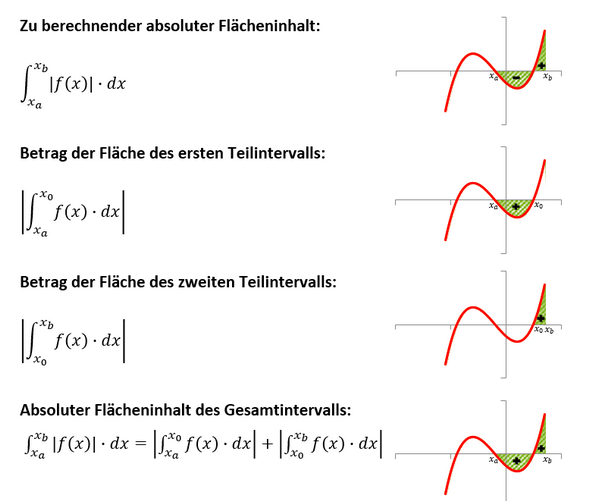
Graphische Veranschaulichung der Berechnung des absoluten Flächeninhalts eines Intervalls:
Video "Absoluter Flächeninhalt":
Das Probe-Video behandelt die Thematik "Absoluter Flächeninhalt" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Anwendung der Berechnung des absoluten Flächeninhalts:
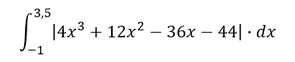
1. Schritt: Ermittlung der Nullstellen, wobei eine Nullstelle mit -1 bekannt ist:
Durch die bekannte Nullstelle kann eine Polynomdivision durchgeführt werden, damit aus der Funktion 3. Grades eine Funktion 2. Grades wird, womit wir die Nullstellen mit der PQ-Formel ermitteln können:
2. Schritt: Prüfen ob die Nullstellen innerhalb des Intervalls liegen und Aufteilung des Intervalls in Teilintervalle:
𝑁𝑢𝑙𝑙𝑠𝑡𝑒𝑙𝑙𝑒𝑛 (−4,4641 ; −1 ; 2,4641)
Die Nullstelle -4,4641 liegt außerhalb des Intervalls und ist irrelevant. Die Nullstelle -1 entspricht schon der unteren Integrationsgrenze. Nur bei der Nullstelle 2,4641 (2,4641<3,5) muss das Intervall geteilt werden.
3. Schritt: Aufteilung des Intervalls in Teilintervalle und Berechnung:
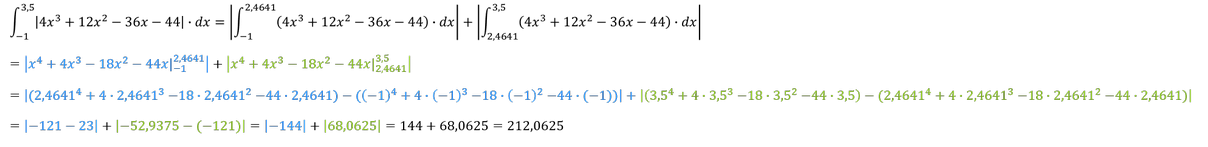
Der absolute Flächeninhalt des Intervalls beträgt 𝟐𝟏𝟐,𝟎𝟔𝟐𝟓
Grundlagen Wirtschaftsmathematik-Paket
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)
21 h Lehrvideos
254 SkriptseitenDas Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
