Cohen Kappa - Vertiefung der Statistik - Fernuni Hagen
Vertiefung Statistik-Paket > Vertiefung-Statistik > Zusammenhangsanalysen nach Skalenniveaus
Grundlagen des Cohen-Kappa-Koeffizienten:
Die Überprüfung von a priori Hypothesen (Hypothesen die vor Datenerhebung aus inhaltlichen Theorien aufgestellt wurden) erfolgt mit Hilfe des Cohen-Kappa-Koeffizienten 𝜅. Der Cohen-Kappa vergleicht dazu die tatsächlich beobachteten Übereinstimmungen des Zusammenhangs mit den Übereinstimmungen, die durch Zufall bei Unabhängigkeit eingetreten wären und setzt diese ins Verhältnis zur perfekten Übereinstimmung abzüglich der zufälligen Übereinstimmung. Dabei kann der Cohen-Kappa Werte bis zur Zahl „1“ annehmen, wobei Werte nahe 1 auf eine fast vollständige Übereinstimmung des vermuteten Zusammenhangs hindeuten.
Merke: Der Cohen-Kappa kann auch negative Werte annehmen, die darauf Hinweisen, dass die Übereinstimmung noch kleiner als die zufällige Übereinstimmung ist.
Allgemeine Berechnung des Cohen-Kappa-Koeffizienten:
Die allgemeine Berechnung des Cohen-Kappa kann über die Summe der relativen Häufigkeiten der als „Wahr (1)“-markierten Zellen (bezeichnet mit 𝐺 für good/gültig) oder der „Fehler (0)“-markierten Zellen (bezeichnet mit 𝐹 für false/Fehler) der Wahrheitstafel erfolgen. Dabei ist zu unterscheiden, ob die Summe der relativen Häufigkeiten den beobachteten (empirischen) Daten (bezeichnet mit einem Plus „+“) oder der Summe der relativen Häufigkeiten bei Unabhängigkeit (bezeichnet mit einem Minus „−“) entstammt:
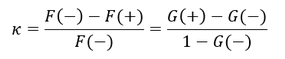
𝐹(+): Summe der relativen Häufigkeiten der „Fehler (0)“-markierten Zellen (𝐹) der empirischen Daten (+)
𝐹(−): Summe der relativen Häufigkeiten der „Fehler (0)“-markierten Zellen (𝐹) bei Unabhängigkeit (−)
𝐺(+): Summe der relativen Häufigkeiten der „Wahr (1)“-markierten Zellen (𝐺) der empirischen Daten (+)
𝐺(−): Summe der relativen Häufigkeiten der „Wahr (1)“-markierten Zellen (𝐺) bei Unabhängigkeit (−)
Merke: Die Berechnung des Cohen-Kappa erfolgt am einfachsten über die „Wahr (1)“-markierten Zellen (𝐺). Das jedoch auch eine Berechnung über die „Fehler (0)“-markierten Zellen (𝐹) erfolgen kann, ist hier nur der Vollständigkeit halber erwähnt.
Unabhängigkeitstafel zur Berechnung des Cohen-Kappa-Koeffizienten:
Da zur Ermittlung des Cohen-Kappa-Koeffizienten die Berechnung der relativen Häufigkeiten des Datenmaterials bei Unabhängigkeit zwingend erforderlich ist, sollte neben der Tabelle mit den empirischen Daten immer eine Unabhängigkeitstafel berechnet werden, in der über die Randverteilung der empirischen Daten die absoluten bzw. relativen Häufigkeiten der Merkmalskombination bei Unabhängigkeit berechnet werden. Die Unabhängigkeitstafel des folgenden beispielhaften empirischen Datenmaterials soll kurz zur Veranschaulichung ermittelt werden:
Video "Cohen Kappa":
Das Probe-Video behandelt die Thematik "Cohen Kappa" des Kurses "Vertiefung der Statistik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Rechenschritte zur Berechnung des Cohen-Kappa-Koeffizienten 𝜿:
Die mathematische Vorgehensweise zur Berechnung des Cohen-Kappa lässt sich am besten anhand eines Rechenbeispiels erläutern. Allgemein lässt sich die Vorgehensweise aber in folgende Schritte unterteilen:
- Umwandlung des Datenmaterials in relative Häufigkeiten (sofern absolute Häufigkeiten angegeben sind)
- Aufstellen der Hypothese in Tabellenform/Wahrheitstafel (A priori-Regel)
- Berechnung der Unabhängigkeitstafel in absoluter und relativer Häufigkeit
- Berechnung des Cohen-Kappa-Koeffizienten über die Summe der „wahr (1)“-markierten relativen Häufigkeiten
Rechenbeispiel für den Cohen-Kappa-Koeffizienten 𝜿:
Ein Unternehmen hat folgende Daten über die Kundenzufriedenheit in zwei Filialen erhoben. Es soll untersucht werden, ob die Zufriedenheit der Filialen übereinstimmt:
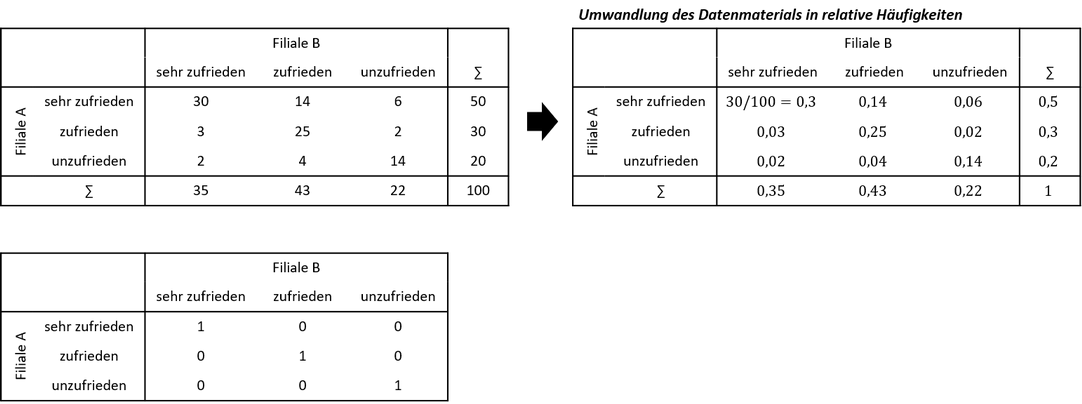
Wir wollen das Beispiel mit Hilfe der Tabellen fortführen, wobei wir nach Aufstellung der Hypothese die relativen Häufigkeiten in den zu „wahr (1)“-markierenden Zellen rot darstellen wollen:
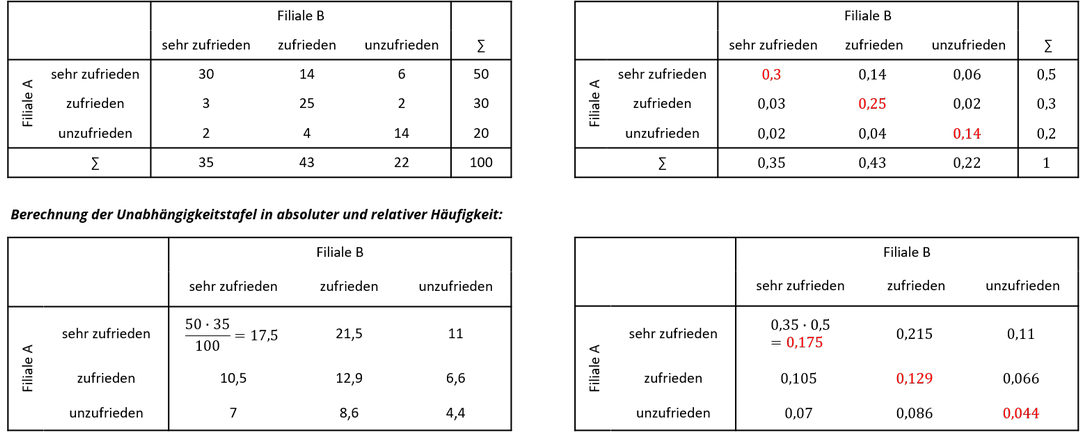
Berechnung des Cohen-Kappa-Koeffizienten κ:
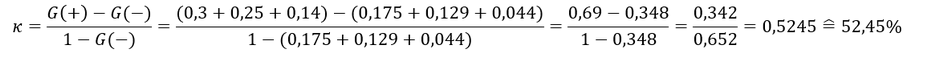
Merke: Der Cohen-Kappa-Koeffizient kann hier als PRE-Maß, also als Gütemaß der Hypothese angesehen werden und gibt die proportionale Fehlerreduktion an.
Vertiefung Statistik-Paket
171 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)
18,5 h LehrvideosDas Vertiefung Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Vertiefung der Statistik" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 140 Übungsaufgaben, Übungsklausuren und zur Auffrischung statistischer Grundkenntnisse das "Grundlagen Statistik-Paket" zur Verfügung.
