Cramers v - Vertiefung der Statistik - Fernuni Hagen
Vertiefung Statistik-Paket > Vertiefung-Statistik > Zusammenhangsanalysen nach Skalenniveaus
Grundlagen der Zusammenhangsmaße nominalskalierter Merkmale:
Die Zusammenhangsmaße für nominalskalierte Merkmale befinden sich auf dem niedrigsten Skalenniveau, können aber natürlich auch für alle Merkmale eines höheren Skalenniveaus berechnet werden. Die Aussagekraft der verschiedenen Kenngrößen ist allerdings sehr gering. Mit Hilfe der Kenngrößen kann lediglich die Aussage über die Stärke eines Zusammenhangs zwischen den Merkmalen getroffen werden. Informationen über die Art und Form (positiv, negativ, linear, monoton, etc.) des Zusammenhangs liefern Zusammenhangsmaße nominalskalierter Merkmale jedoch nicht.
Chi-Quadrat-Koeffizient 𝝌^𝟐:
Der Chi-Quadrat-Koeffizient 𝜒^2 ist der Ausgangspunkt für alle weiteren Zusammenhangsmaße nominalskalierter Merkmale. Die Kenngröße prüft den Zusammenhang zwischen den Merkmalen, ist jedoch nur nach unten auf die Zahl 0 begrenzt, wohingegen es nach oben keinerlei Begrenzung gibt. Das macht den Chi-Quadrat-Koeffizienten schwer interpretierbar, weshalb alle anderen Kennzahlen lediglich versuchen, den Chi-Quadrat-Koeffizienten auf verschiedene Weise auf den Bereich von 0 und 1 zu normieren, um eine leichtere Interpretation für die Stärke des Zusammenhangs zu ermöglichen. Die Berechnung des Chi-Quadrat-Koeffizient erfolgt über die absoluten Häufigkeiten bei Unabhängigkeit, weshalb er am leichtesten nach Erstellung einer Unabhängigkeitstafel berechnet werden kann. Allgemein gilt für den Koeffizienten:
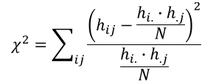
Kontingenzkoeffizient 𝑲:
Der Kontingenzkoeffizient lässt sich mit Hilfe des Chi-Quadrat-Koeffizienten ermitteln und normiert diesen. Dennoch bedarf es einer weiteren Korrektur des Kontingenzkoeffizienten, damit dieser wirklich Werte zwischen 0 und 1 annimmt, wobei Werte nahe 1 auf einen starken und Werte nahe 0 auf einen schwachen oder keinen Zusammenhang hindeuten. Der Kontingenzkoeffizient errechnet sich allgemein wie folgt:
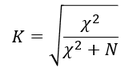
Phi-Koeffizient 𝝓:
Der Phi-Koeffizient normiert ebenfalls den Chi-Quadrat-Koeffizienten auf Werte zwischen 0 und 1. Er kann allerdings nur im Falle einer Kreuztabelle mit lediglich vier Feldern (Vierfeldertafel) verwendet werden, also nur für dichotome Merkmale, die auf zwei Merkmalsausprägungen begrenzt sind. Der Koeffizient errechnet sich allgemein wie folgt:
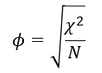
Cramérs 𝒗:
Cramérs 𝑣 normiert, wie der Phi-Koeffizient, ebenfalls den Chi-Quadrat-Koeffizienten auf Werte zwischen 0 und 1, kann aber für nominalskalierte Merkmale mit beliebig vielen Merkmalsausprägungen verwendet werden. Im Fall nur zweier Merkmalsausprägungen stimmen Cramérs 𝑣 und der Koeffizient 𝜙 überein. Cramérs 𝑣 errechnet sich allgemein wie folgt:

Video "Cramers v":
Das Probe-Video behandelt die Thematik "Cramers v" des Kurses "Vertiefung der Statistik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Rechenbeispiel für die Zusammenhangsmaße 𝝌^𝟐, 𝑲, 𝝓, 𝒗:
Mit Hilfe eines Beispiels wollen wir uns die Berechnung der einzelnen Zusammenhangsmaße 𝜒^2, 𝐾, 𝜙, 𝑣 nochmals veranschaulichen. Dabei wollen wir von der bereits bekannten Kreuztabelle mit den Merkmalen Geschlecht und Umweltbewusstsein ausgehen, wobei wir direkt daneben die Unabhängigkeitstafel berechnen wollen, die wir zur Berechnung des Chi-Quadrat-Koeffizienten benötigen:

Berechnung des Chi-Quadrat-Koeffizienten 𝝌^𝟐: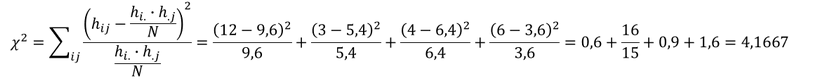
Mit Hilfe der Unabhängigkeitstafel lässt sich 𝜒^2 sehr leicht berechnen. Die jeweiligen Häufigkeiten bei Unabhängigkeit sind von den jeweiligen empirischen Häufigkeiten abzuziehen zu quadrieren und durch die jeweiligen Häufigkeiten bei Unabhängigkeit erneut zu dividieren. Die Summe aller Quotienten ergibt die Kenngröße 𝜒^2:
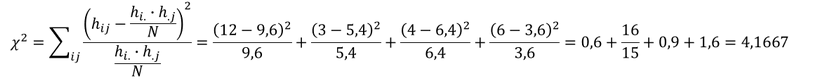
Berechnung des Kontingenzkoeffizienten 𝑲: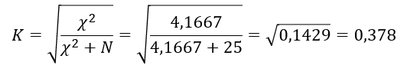
Zur Berechnung des Kontingenzkoeffizienten ist die Wurzel aus dem Quotienten der Kenngröße 𝜒^2 durch 𝜒^2 plus der Anzahl der Beobachtungswerte zu ziehen:
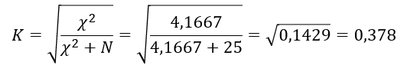
Berechnung des Phi-Koeffizienten 𝜙: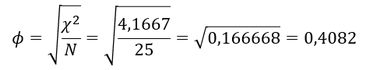
Da es sich um eine Vierfeldertafel handelt, kann 𝜙 berechnet werden. Dazu ist die Wurzel aus dem Quotienten 𝜒^2 durch die Anzahl der Beobachtungswerte zu ziehen:
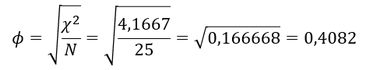
Berechnung des Cramérs 𝒗: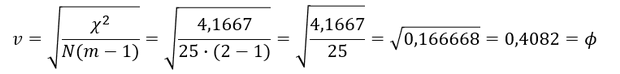
Zur Berechnung von 𝑣 ist die Wurzel aus dem Quotienten 𝜒^2 durch die Anzahl der Beobachtungswerte multipliziert mit der minimalen Anzahl an Zeilen/Spalten minus 1 zu ziehen:
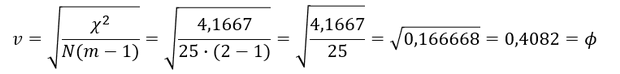
Vertiefung Statistik-Paket
Das Vertiefung Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Vertiefung der Statistik" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 140 Übungsaufgaben, Übungsklausuren und zur Auffrischung statistischer Grundkenntnisse das "Grundlagen Statistik-Paket" zur Verfügung.


