Elastizität - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Differentialrechnung
Definition der Elastizität:
Die Elastizität gibt das Verhältnis einer relativen Veränderung (prozentuale Veränderung) des 𝑥-Faktors zur relativen Veränderung des Funktionswertes (𝑓(𝑥)) an.
Erklärung der Elastizität:
Die Elastizität trifft damit eine ökonomische Aussage darüber, wie sich eine prozentuale Änderung eines bestimmten Faktors auf den Funktionswert auswirkt.
Nehmen wir als Beispiel eine Kostenfunktion 𝐾(𝑥), welche abhängig von der produzierten Menge 𝑥 ist. Erhöht man die Produktionsmenge, so steigen auch die Kosten.
Beispiel:
𝐾(𝑥) = 3𝑥 + 7
Kosten bei der Produktion von 3 Mengeneinheiten (𝑥 = 3):
𝐾(3) = 3 ∙ 3 + 7 = 16
Steigert man nun die Produktionsmenge auf 5 Mengeneinheiten (𝑥=5) steigen gleichzeitig entsprechend die Kosten:
𝐾(5) = 3 ∙ 5 + 7 = 22
Die errechneten Werte der Kosten 16 und 22 stellen die absolute Veränderung des Funktionswertes dar, da wir die Mengeneinheiten von 𝑥 um einen absoluten Wert von 2 gesteigert haben.
Mittels der Elastizität soll nun aber herausgefunden werden, wie der Kostenwert sich prozentual (relativ) verändert, wenn man eine prozentuale (relative) Veränderung der Produktionsmenge vornimmt.
Um wie viel Prozent verändern sich die Kosten, wenn man die Produktionsmenge um 1% erhöht?
Diesen Zusammenhang beschreibt die Elastizität.
!!! ACHTUNG!!!
Je nach Funktionsverlauf kann die Elastizität an unterschiedlichen Stellen auch unterschiedlich ausfallen
Mathematische Bestimmung der Elastizität:
Mathematisch lässt sich das Verhältnis einer relativen Veränderung des 𝑥-Wertes zur relativen Veränderung des Funktionswertes wie folgt bestimmen:
Die Elastizität an der Stelle 𝒙_𝟎 beschreibt, um wie viel Prozent sich der Funktionswert ändert, wenn 𝒙_𝟎 um 1 Prozent erhöht wird.
Beispiel: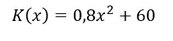
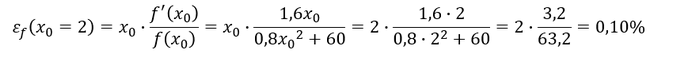
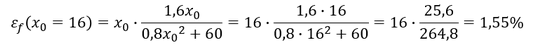
Gegeben sei folgende Kostenfunktion 𝐾(𝑥):
Die Elastizität für die Stelle 𝑥_0 = 2 (2 Mengeneinheiten) lautet:
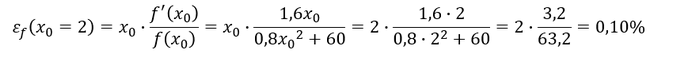
Steigert man die Produktionsmenge von 2 um 1%, steigen die Kosten lediglich um 0,10%
Beweis:
Die Elastizität kann je nach Funktionsverlauf unterschiedlich ausfallen!
Prüfung der Elastizität an der Stelle 𝒙_𝟎 = 𝟏𝟔:
Steigert man die Produktionsmenge von 16 um 1%, steigen die Kosten um 1,55%.
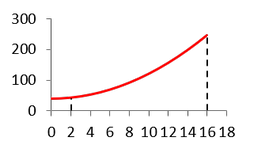
Der Grund dieser Steigerung liegt darin, dass die Kostenfunktion streng konvex steigend verläuft.
Video "Elastizität":
Das Probe-Video behandelt die Thematik "Elastizität" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Grundlagen Wirtschaftsmathematik-Paket
Klausurlösungen
Live-Webinare
Übungen (optional)
21 h Lehrvideos
254 Skriptseiten
FormelsammlungDas Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
