Integrieren - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Integrale
Bedeutung der Stammfunktion:
Bei der Stammfunktion 𝐹(𝑥) handelt es sich um eine Funktion, welche abgeleitet eine beliebige aber vorgegebene reelle Funktion 𝑓 ergibt. Zur Ermittlung einer Stammfunktion muss die angegebene Funktion „aufgeleitet“ bzw. integriert werden. Dazu ist genau der gegenteilige Prozess zur Ableitung zu vollziehen. Leitet man die Stammfunktion wiederrum ab, muss sie der vorgegebenen reellen Funktion 𝑓 entsprechen.
Mathematische Durchführung einer Integration:
Zur Aufleitung bzw. Integration einer Funktion 𝑓 muss der Exponent mit der Zahl 1 addiert werden. Danach muss der Kehrwert des Exponenten mit der davorstehenden Zahl multipliziert werden. Zusätzlich ist IMMER eine Konstante c hinzuzuaddieren, da diese bei einer entsprechenden Ableitung wegfallen würde. Die grundsätzliche Integration einer Funktion soll mit folgender Funktion veranschaulicht werden:
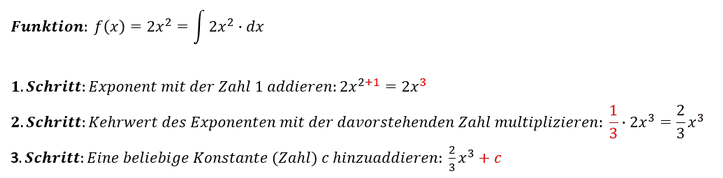
Die Integration lautet folglich:
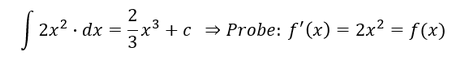
Beispiele:
Video "Integrieren":
Das Probe-Video behandelt die Thematik "Integrieren" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Integrationsregeln bei Additionen und Subtraktionen:
Bei Funktionen mit Additionen oder Subtraktionen wird im Ablauf genau gleich verfahren, jedoch muss jede einzelne Variable der Funktion integriert werden. Es ist der gleiche Prozess wie beim Ableiten, eben nur umgekehrt, vorzunehmen.
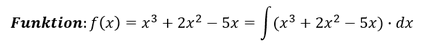
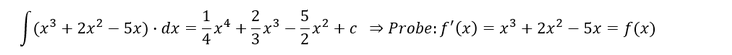
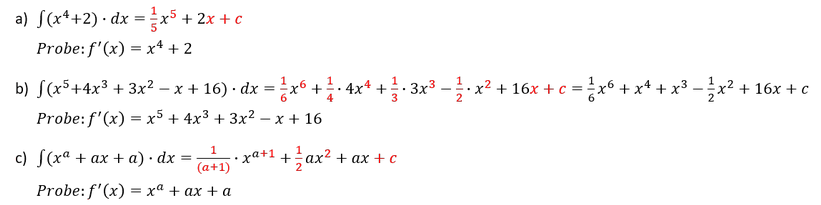
Integration einer Funktion mit Additionen und Subtraktionen:
Folgende Funktion sei gegeben, welche es nach 𝑥 zu integrieren gilt:
Die Terme sind nach dem eben genannten Schema einfach zu integrieren, dabei bleiben + oder – unverändert, sofern der Exponent positiv ist:
Die Integration lautet folglich:
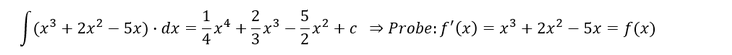
Beispiele:
Grundlagen Wirtschaftsmathematik-Paket
Live-Webinare
Übungen (optional)
21 h Lehrvideos
254 Skriptseiten
Formelsammlung
KlausurlösungenDas Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
