Konvergente Folge - Divergente Folge - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Folgen und Reihen
Konvergenz:
Strebt eine Folge nach einer Zahl (auch Null), wird diese Folge als konvergent bezeichnet. Die Folge besitzt eine Grenze. Berechnet man den Grenzwert, erhält man eine eindeutige Zahl (Eindeutiger Grenzwert).
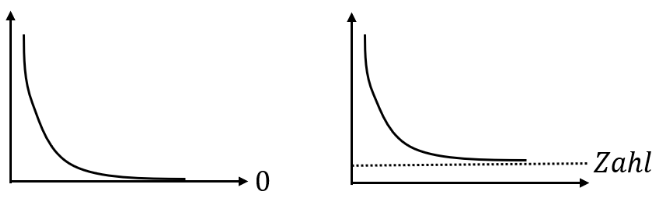
Eine Folge ist konvergent, wenn sie eine Grenze besitzt bzw. nicht in die Unendlichkeit verläuft. Die Grenze erhält man durch die Grenzwert-Berechnung.
1. Beispiel:
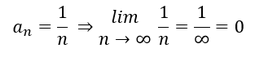
Diese Folge besitzt eine Grenze bei der Zahl Null. Die Folge konvergiert gegen 0.
2. Beispiel:
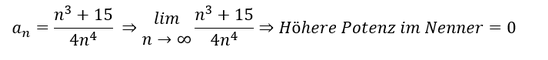
Diese Folge besitzt ebenfalls eine Grenze bei der Zahl Null. Die Folge konvergiert gegen 0.
3. Beispiel:
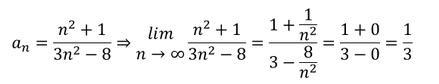
Diese Folge besitzt eine Grenze bei der Zahl 1/3 . Die Folge konvergiert gegen 1/3.
Alle Beispielfolgen werden als konvergent bezeichnet, da sie eine bestimmte Grenze besitzen und eine eindeutige Aussage getroffen werden kann, welchen Wert die Folge erreicht, wenn die Zahl unendlich groß wäre.
Video "Konvergente Folge":
Das Probe-Video behandelt die Thematik "Konvergente Folge - Divergente Folge" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Divergenz:
Strebt eine Folge nicht nach einer Zahl, wird diese Folge als divergent bezeichnet. Die Folge besitzt keine Grenze. Berechnet man den Grenzwert, gelangt man zu ±∞. Alle Folgen, die nicht konvergent sind, sind divergent.
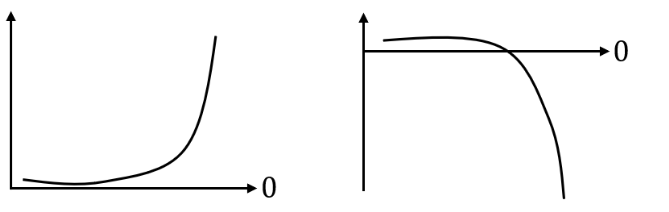
Eine Folge ist divergent, wenn sie keine Grenze besitzt bzw. in die Unendlichkeit verläuft.
1. Beispiel:
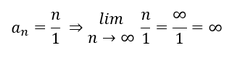
Diese Folge besitzt keine Grenze. Die Folge ist divergent.
2. Beispiel:
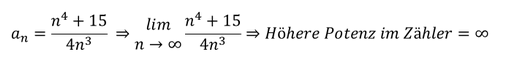
Diese Folge besitzt keine Grenze. Die Folge ist divergent.
3. Beispiel:
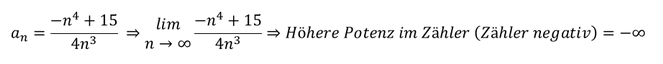
Diese Folge besitzt keine Grenze. Die Folge ist divergent.
Alle Beispielfolgen werden als divergent bezeichnet, da sie keine bestimmte Grenze besitzen und keine eindeutige Aussage darüber getroffen werden kann, welchen Wert die Folge erreicht, wenn die Zahl unendlich groß wäre.
Grundlagen Wirtschaftsmathematik-Paket
254 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)
21 h LehrvideosDas Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
