Prognoseintervall - Vertiefung der Statistik - Fernuni Hagen
Vertiefung Statistik-Paket > Vertiefung-Statistik > Regressionsanalyse
Grundlagen des Prognose-Intervalls (Vorhersage-Intervall) für 𝒀_𝟎:
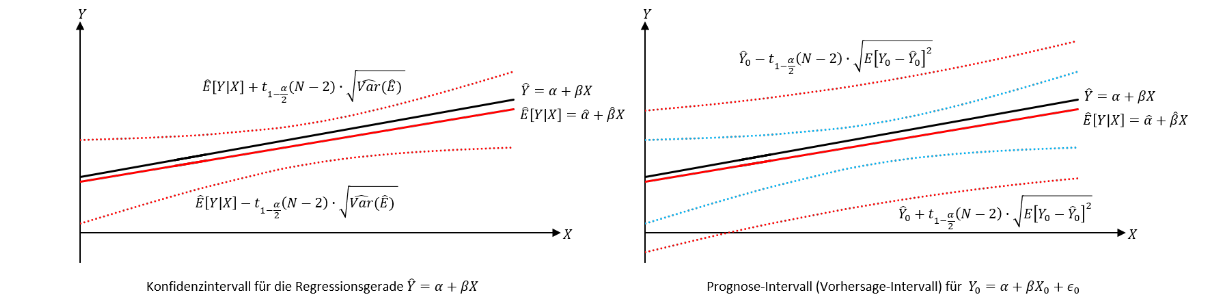
Mit Hilfe des Konfidenzintervalls der Regressionsgeraden können Intervalle für beliebige 𝑋-Werte ermittelt werden, die die wahre Regressionsgerade und damit den von der wahren Regressionsgeraden ermittelten Prognosewert 𝑌 ̂ mit einer Wahrscheinlichkeit von 1− 𝛼 überdecken. Da jedoch die wahren zu beobachtenden 𝑌-Werte nicht auf der wahren Regressionsgeraden liegen, sondern um die Gerade schwanken, kann keine Wahrscheinlichkeitsaussage über einen bestimmten wahren unbekannten 𝑌_0-Wert getroffen werden. Deshalb bedarf es eines sogenannten Prognose-Intervalls, welches zusätzlich auch die Schwankung der wahren Y-Werte um die wahre Regressionsgerade bzw. die Fehler 𝜖_𝑛 berücksichtigt und damit die wahren unbekannten 𝑌-Werte, bzw. den wahren unbekannten 𝑌_0-Wert mit einer Wahrscheinlichkeit von 1− 𝛼 überdeckt.
Konzept hinter dem Prognose-Intervall für 𝒀_𝟎:
Das Prognose-Intervall (Vorhersage-Intervall) baut auf dem Konfidenzintervall für die Regressionsgerade auf. Die verschiedenen Intervallgrenzen des Konfidenzintervalls für die Regressionsgerade geben die möglichen äußersten Prognosewerte 𝑌 ̂ bei einer Irrtumswahrscheinlichkeit von 1"−" 𝛼 der wahren Regressionsgeraden an. Ergänzt man diese möglichen äußersten Prognosewerte zusätzlich um die geschätzte Varianz der Regressionsgeraden, also um die Streuung der wahren 𝑌-Werte um die Regressionsgerade, gelangt man zum Prognose-Intervall. Da es sich bei der geschätzten Varianz der wahren Werte um die wahre Regressionsgerade um den Varianz-Schätzer 𝜎 ̂^2 handelt, ist dieser einfach nochmal zusätzlich in der Formel für die Intervallgrenzen des Konfidenzintervalls zu berücksichtigen, indem man den Wert 1 zusätzlich in die Wurzel bei der Varianz schreibt:
Merke: Das Prognose-Intervall ist mit der zusätzlichen Berücksichtigung des Varianz-Schätzers immer größer als das Konfidenzintervall der Regressionsgeraden. Ein bestimmter Beobachtungswert 𝑌_0 wird dafür aber dann mit einer Wahrscheinlichkeit von 1-𝑎 vom Prognose-Intervall überdeckt.
Video "Prognoseintervall":
Das Probe-Video behandelt die Thematik "Prognoseintervall" des Kurses "Vertiefung der Statistik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Allgemeine Berechnung des Prognose-Intervall für 𝒀_𝟎:
Ausgangspunkt des Prognose-Intervalls stellt der 𝑌_0-Wert dar, wobei sich dieser wiederrum mittels der geschätzten linearen Regressionsfunktion bei einem beliebigen aber eindeutigen 𝑋_0-Wert ermitteln lässt und sich deshalb eigentlich nicht vom Ausgangspunkt des Konfidenzintervalls für die Regressionsgerade 𝐸 ̂[𝑌|𝑋] unterscheidet. Die Bildung des Konfidenzintervalls erfolgt auf gleiche Weise, wie bei dem Konfidenzintervall der Regressionsgeraden, mittels der Student t-Verteilung, allerdings mit dem Unterschied, dass der zu erwartende quadrierte Prognose-Fehler 𝐸[𝑌_0−𝑌 ̂_0 ]^2 als Varianz zu verwenden ist. Das zweiseitige Konfidenzintervall, wobei das Gleiche für einseitige Konfidenzintervalle nur mittels einer Grenze und 1−𝑎 gilt, kann wie folgt gebildet werden:
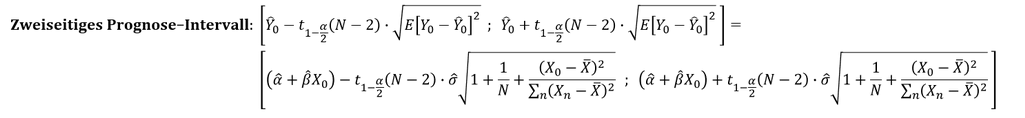
Merke: Alle Variablen bis auf die freie Wahl der Variablen 𝑋_0 werden aus der ursprünglichen Stichprobe, mittels derer auch die Schätzer 𝛼 ̂ und 𝛽 ̂ berechnet wurden, gewonnen.
Beispielberechnung eines zweiseitigen Prognose-Intervalls:
Aus einer Stichprobe im Umfang von 𝑁 = 20 ließen sich die folgenden Schätzwerte 𝛼 ̂, 𝛽 ̂ und die dazugehörigen Varianzen für ein lineares Regressionsmodell ermitteln. Es soll das zweiseitige Prognose-Intervall an der Stelle 𝑋_0 = 400 bei einer Irrtumswahrscheinlichkeit von 𝛼 = 0,05 ermittelt werden:
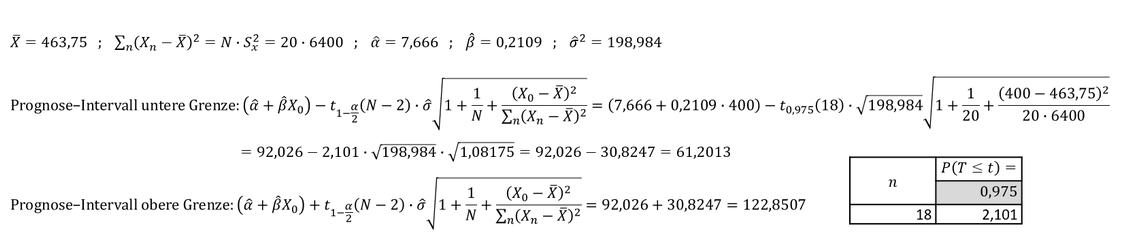
Das Prognose-Intervall (Vorhersage-Intervall) an der Stelle 𝑋_0 = 400 lautet [61,2013 ; 122,8507].
Merke: Auch das Prognose-Intervall wäre an der Stelle 𝑋 = 463,75 minimal, da der gewählte 𝑋_0-Wert und der Erwartungswert übereinstimmen würden. Die Varianz unter der Wurzel würde folglich nur noch 1+1/𝑁 betragen.
Vertiefung Statistik-Paket
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Vertiefung Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Vertiefung der Statistik" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 140 Übungsaufgaben, Übungsklausuren und zur Auffrischung statistischer Grundkenntnisse das "Grundlagen Statistik-Paket" zur Verfügung.
18,5 h Lehrvideos
171 Skriptseiten