Rang einer Matrix - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Lineare Algebra
Rang einer Matrix:
Der Rang einer Matrix (𝑟𝑔) entspricht der Anzahl an linear unabhängigen Vektoren innerhalb der Matrix. Das bedeutet, um den Rang der Matrix bestimmen zu können, ist die Matrix auf lineare Unabhängigkeit der Vektoren zu prüfen.
Maximaler Rang einer Matrix:
Der maximale Rang einer Matrix entspricht der kleineren Anzahl an Zeilen- oder Spaltenvektoren der Matrix:
𝑚 > 𝑛 ⇒ 𝑅𝑎𝑛𝑔 (𝑟𝑔) ≤ 𝑛
𝑚 < 𝑛 ⇒ 𝑅𝑎𝑛𝑔 (𝑟𝑔) ≤ 𝑚
𝑚 = 𝑛 ⇒ 𝑅𝑎𝑛𝑔 (𝑟𝑔) ≤ 𝑚 𝑏𝑧𝑤. 𝑛
Natürlich kann der Rang auch geringer ausfallen, wenn weniger als 𝑚 oder 𝑛 Vektoren innerhalb der Matrix linear unabhängig voneinander sind.
Ermittlung des Rangs einer Matrix:
Zur Ermittlung, wie viele Vektoren der Matrix linear unabhängig voneinander sind, ist die Matrix in eine obere Dreiecksmatrix (spezielle Matrix) umzuwandeln. Die Umwandlung der Matrix in eine obere Dreiecksmatrix erfordert die Nutzung des Gauß-Algorithmus, denn der Gauß-Algorithmus besagt, dass bei den folgenden Veränderungen innerhalb der Matrix, der Rang der Matrix unverändert bleibt:
- Beim Vertauschen von Zeilen der Matrix
- Beim Vertauschen von Spalten der Matrix
- Bei der Multiplikation einer Zeile mit einer reellen Zahl ≠ 0
- Bei der Addition eines Vielfachen einer Zeile zu einer anderen Zeile (gilt auch für Subtraktion)
Vorgehensweise der zur Ermittlung des Rangs einer Matrix:
Um zur oberen Dreiecksmatrix zu gelangen, müssen alle Spalten unterhalb der Diagonalen der Matrix eine 0 aufweisen. Dazu müssen Umformungen vorgenommen werden.
Zur Darstellung der Vorgehensweise seien folgende Matrizen unterstellt. Dabei wird die jeweilige Zeile einer Matrix mit I, II, III, usw. beschrieben.
1. Schritt: Prüfung, ob die erste reelle Diagonalzahl mit „0“ notiert ist. Ist dies der Fall, so ist die Zeile mit einer Anderen zu vertauschen, in dessen erster Spalte keine 0 steht.
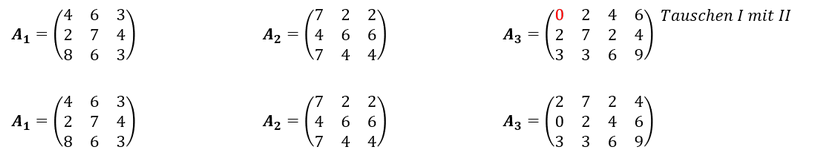
2. Schritt: Der Spaltenvektor, in dem die Diagonalzahl steht, darf bis auf die Diagonalzahl nur Nullen aufweisen. Dazu ist die Zeile mit der Diagonalzahl mit einem jeweiligen Vielfachen zu multiplizieren und von den anderen Zeilen abzuziehen. Das jeweilige Vielfache ergibt sich als Bruch aus den reellen Zahlen des Spaltenvektors die zu 0 werden sollen als Zähler und der diagonalen Zahl als Nenner.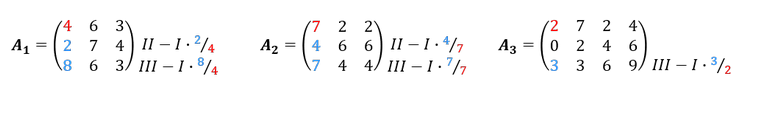
Video "Rang einer Matrix":
Das Probe-Video behandelt die Thematik "Rang einer Matrix" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Ablesen des Rangs einer Matrix:
Der Rang einer Matrix, welche sich in der oberen Dreiecksform befindet, entspricht der Anzahl an Zeilen, welche nicht ausschließlich aus Nullen bestehen.
Aus unseren Berechnungen haben sich folgende Matrizen ergeben:
Weitere Beispiele:
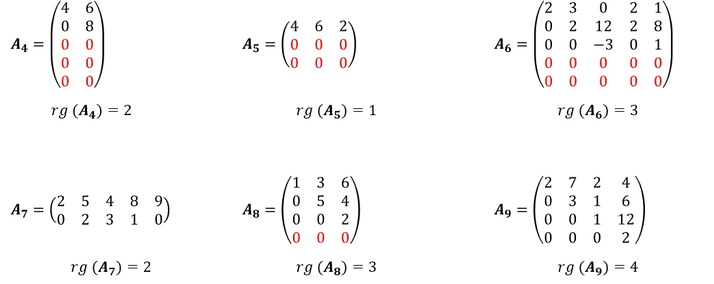
Zur Bestimmung des Rangs sind ausschließlich die Zeilen zu zählen, bei denen es sich nicht um Nullzeilen handelt.
Grundlagen Wirtschaftsmathematik-Paket
Live-Webinare
Übungen (optional)
21 h Lehrvideos
254 Skriptseiten
Formelsammlung
KlausurlösungenDas Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
