Simplex Algorithmus - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Lineare Gleichungssysteme & Optimierung
Lösung mittels Simplex-Algorithmus:
Die Lösung mittels Simplex-Algorithmus erfolgt über Pivotschritte. Dabei wird, wie bereits bei der Lösung von Gleichungssystemen kennengelernt, eine komplette Spalte zu 0 umgeformt, bis auf eine Zahl innerhalb der Spalte, in welcher die Zahl 1 entstehen soll. Dabei bezeichnet man die Zeile in der die Zahl 1 entstehen soll als Pivotzeile und die entsprechende Spalte als Pivotspalte. Dort wo sich Pivotzeile und Pivotspalte kreuzen, befindet sich das Pivotelement, also die Zahl, welche zu 1 umgeformt werden soll. Beim Simplex-Algorithmus geht es nun aber nicht darum, das Tableau in eine Einheitsmatrix umzuformen, sondern es werden nur Umformungen in den Spalten vorgenommen, in denen die Zielfunktion negative Werte aufweist. Sobald die Zielfunktion in ihrer gesamten Zeile keine negativen Werte mehr aufweist, haben wir das Optimum gefunden.
Allgemeine Vorgehensweise zur Lösung mittels Simplex-Algorithmus:
Schritt 1: In der Zielfunktion ist die höchste negative Zahl zu suchen. Bei der Spalte, in der die höchste negative Zahl gelistet ist, handelt es sich um die Pivotspalte, diese ist zu markieren.
Schritt 2: Die Ergebnisse in der RHS-Spalte sind durch ihre jeweiligen reellen Zahlen der Nebenbedingungen aus der Pivotspalte zu dividieren und die Ergebnisse rechts von der RHS-Spalte in Dezimalschreibweise zu notieren.
Schritt 3: Es ist das Ergebnis aus der Berechnung von Schritt 2 zu suchen, welches am geringsten, aber positiv ist. Bei der Zeile, in der das geringsten Ergebnis steht, handelt es sich um die Pivotzeile.
Schritt 4: Es ist die Zahl einzukreisen, bei der sich Pivotspalte und Pivotzeile kreuzen.
Schritt 5: Die Pivotspalte ist bis auf das Pivotelement zu Nullen umzuformen. Das Pivotelement ist zu 1 umzuformen. Die Vorgehensweise erfolgt dabei wie beim gelernten Gleichungssystem.
Diese Schritte sind solange zu wiederholen, bis in der Zielfunktion keine negativen Zahlen mehr auftauchen. Ist dies der Fall, gilt das Tableau als gelöst und wir können die Werte, die zum Gewinnmaximum führen aus dem Tableau ablesen.
!!!ACHTUNG!!!
Tauchen in der Pivotspalte ausschließlich negative Zahlen auf, ergeben sich keine positiven Zahlen bei der Division, in diesem Fall existiert keine optimale Lösung für das Tableau.
Lösung des linearen Programmes:
Wir wollen nun mittels des Simplex-Algorithmus unser lineares Beispielprogramm lösen.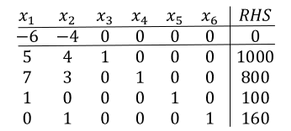
Schritt 1: Suchen der höchsten negativen Zahl in der Zielfunktion und Markieren der entsprechenden Spalte (Pivotspalte).
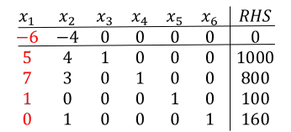
Schritt 2: Die Ergebnisse in der RHS Spalte sind durch die reellen Zahlen der Nebenbedingungen aus der Pivotspalte zu dividieren.
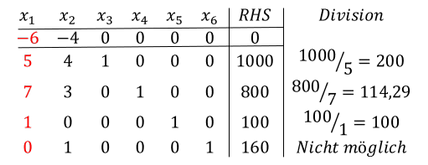
Schritt 3: Suchen des geringsten Divisionsergebnisses und Markieren der entsprechenden Zeile (Pivotzeile).
Schritt 4: Einkreisen der Zahl (Pivotelement), bei der sich Pivotspalte und Pivotzeile kreuzen.
Schritt 5: Die Pivotspalte ist zu Nullen und das Pivotelement zu 1 umzuformen.
Die Schritte sind nun erneut zu wiederholen, da die Zielfunktion weiterhin negative Werte aufweist, was bedeutet, dass die Zielfunktion weiter gesteigert werden kann.
Video "Simplex Algorithmus":
Das Probe-Video behandelt die Thematik "Simplex Algorithmus" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Grundlagen Wirtschaftsmathematik-Paket
Klausurlösungen
Live-Webinare
Übungen (optional)
21 h Lehrvideos
254 Skriptseiten
FormelsammlungDas Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
