Stationäre Stelle - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Differentialrechnung
Definition der stationären Stelle:
Um ein Optimum bei zwei oder mehreren Variablen ermitteln zu können, muss eine stationäre Stelle vorhanden sein. Eine stationäre Stelle ist ein Punkt in dem alle Variablen eine Steigung von 0 aufweisen. Eine stationäre Stelle kann dann vielleicht ein Hoch- oder Tiefpunkt sein.
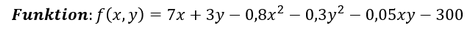
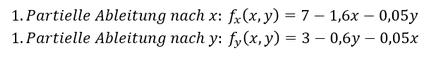
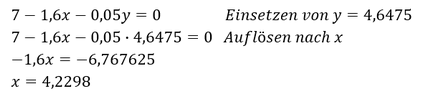
Ermittlung einer stationären Stelle:
Zur Ermittlung einer stationären Stelle wird die Funktion partiell nach den Variablen abgeleitet und gleich null gesetzt. Die partiell abgeleiteten Funktionen müssen sich dann in einem Gleichungssystem lösen lassen. Kann das Gleichungssystem gelöst werden, besteht eine stationäre Stelle.
Mathematische Ermittlung einer stationären Stelle:
Schritt 1: Ermittlung der partiellen Ableitungen:
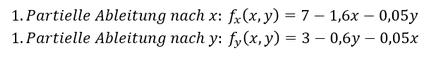
Schritt 2: Nullsetzen der Ableitungen und Auflösen des Gleichungssystems nach 𝑥 oder 𝑦:
Schritt 3: Einsetzen der abgeleiteten Variable in die partielle Ableitung der anderen Funktion und Auflösen nach der anderen Variable:
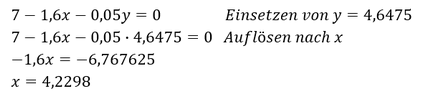
Die Funktion hat eine stationäre Stelle bei 𝒙_𝟎 = 𝟒,𝟐𝟐𝟗𝟖 , 𝒚_𝟎 = 𝟒,𝟔𝟒𝟕𝟓.
Video "Stationäre Stelle":
Das Probe-Video behandelt die Thematik "Stationäre Stelle" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Ermittlung des Hoch- oder Tiefpunktes mit der stationären Stelle:
Um zu ermitteln, ob es sich bei der stationären Stelle tatsächlich um ein Optimum (Hoch- oder Tiefpunkt) handelt, müssen die 2. partiellen Ableitungen und die Kreuzableitung gebildet werden. Die Ermittlung erfolgt durch die Multiplikation der beiden 2. partiellen Ableitung und der Subtraktion der quadrierten Kreuzableitung. Das Ergebnis ist dann auf Positivität zu prüfen und nach der 2. Ableitung nach 𝑥 einzuordnen.
Notwendige Bedingung für ein Optimum:
Die stationäre Stelle ist mit folgender Gleichung zu überprüfen. Ist diese Gleichung positiv, handelt es sich um ein Optimum. Ist die Gleichung hingegen negativ, handelt es sich um einen Sattelpunkt.
Hinreichende Bedingungen:
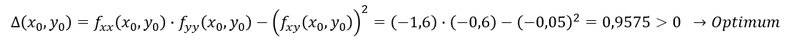
𝐿𝑜𝑘𝑎𝑙𝑒𝑠 𝑀𝑎𝑥𝑖𝑚𝑢𝑚:𝑓_𝑥𝑥 (𝑥_0,𝑦_0 ) < 0
𝐿𝑜𝑘𝑎𝑙𝑒𝑠 𝑀𝑖𝑛𝑖𝑚𝑢𝑚: 𝑓_𝑥𝑥 (𝑥_0,𝑦_0 ) > 0
Mathematische Bestimmung des Optimums:
1. 𝑃𝑎𝑟𝑡𝑖𝑒𝑙𝑙𝑒 𝐴𝑏𝑙𝑒𝑖𝑡𝑢𝑛𝑔 𝑛𝑎𝑐ℎ 𝑥: 𝑓_𝑥 (𝑥,𝑦) = 7 − 1,6𝑥 − 0,05𝑦
1. 𝑃𝑎𝑟𝑡𝑖𝑒𝑙𝑙𝑒 𝐴𝑏𝑙𝑒𝑖𝑡𝑢𝑛𝑔 𝑛𝑎𝑐ℎ 𝑦: 𝑓_𝑦 (𝑥,𝑦) = 3 − 0,6𝑦 − 0,05𝑥
Schritt 4: Bildung der 2. partiellen Ableitungen und der Kreuzableitung
2. 𝑃𝑎𝑟𝑡𝑖𝑒𝑙𝑙𝑒 𝐴𝑏𝑙𝑒𝑖𝑡𝑢𝑛𝑔 𝑛𝑎𝑐ℎ 𝑥: 𝑓_𝑥𝑥 (𝑥,𝑦) = −1,6
2. 𝑃𝑎𝑟𝑡𝑖𝑒𝑙𝑙𝑒 𝐴𝑏𝑙𝑒𝑖𝑡𝑢𝑛𝑔 𝑛𝑎𝑐ℎ 𝑦: 𝑓_𝑦𝑦 (𝑥,𝑦) = −0,6
2. 𝐾𝑟𝑒𝑢𝑧𝑎𝑏𝑙𝑒𝑖𝑡𝑢𝑛𝑔 𝑛𝑎𝑐ℎ 𝑦: 𝑓_𝑥𝑦 (𝑥,𝑦) = −0,05
Schritt 5: Aufstellung der Gleichung und Prüfung der notwendigen Bedingung.
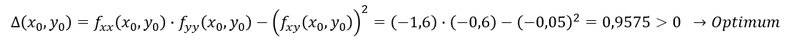
Schritt 6: Prüfung der hinreichenden Bedingung, ob es sich um einen Hoch- oder Tiefpunkt handelt
2. 𝑃𝑎𝑟𝑡𝑖𝑒𝑙𝑙𝑒 𝐴𝑏𝑙𝑒𝑖𝑡𝑢𝑛𝑔 𝑛𝑎𝑐ℎ 𝑥: 𝑓_𝑥𝑥 (𝑥,𝑦) = −1,6 < 0 → 𝐻𝑜𝑐ℎ𝑝𝑢𝑛𝑘𝑡
Die stationäre Stelle 𝒙_𝟎 = 𝟒,𝟐𝟐𝟗𝟖 , 𝒚_𝟎 = 𝟒,𝟔𝟒𝟕𝟓 ist ein lokaler Hochpunkt (Maximum).
Grundlagen Wirtschaftsmathematik-Paket
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)
21 h Lehrvideos
254 SkriptseitenDas Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
