T-Differenztest - Vertiefung der Statistik - Fernuni Hagen
Vertiefung Statistik-Paket > Vertiefung-Statistik > Zweistichproben-Testverfahren
Beispielhafte Aufgabe für den 𝑻-Differenztest (Behrens-Fisher-Problem):
Ein Unternehmen betreibt zwei verschiedene verkaufsfördernde Maßnahmen 𝑋 und 𝑌. Anhand der Umsatzsteigerungen möchte das Unternehmen die Maßnahmen vergleichen, wobei es davon ausgeht, dass die Maßnahme 𝑋 die erfolgreichere ist. Für das normalverteilte Datenmaterial im Umfang von 𝑁, 𝑀 = 4 ergaben sich folgende Statistiken:
𝑋 ̅ = 45,75 ; 𝑌 ̅ = 35,25
𝑆_𝑥^2 = 63,1 ; 𝑆_𝑦^2 = 115,4
Wie lautet die passende Nullhypothese für das statistische Testverfahren und kann die Nullhypothese bei einem Signifikanzniveau von 𝛼 = 0,05 abgelehnt werden?
Lösung 𝑻-Differenztest (Behrens-Fisher-Problem):
Wahl des Testverfahrens
Da zwei Erwartungswerte aus zwei Stichproben verglichen werden sollen, ist ein Differenztest zu wählen. Da die Stichprobenumfänge 𝑁,𝑀<30 sind und die unbekannten Varianzen 𝑆_𝑥^2 = 𝑆_𝑦^2 nicht übereinstimmen, ist der 𝑇-Differenztest mit dem Behrens-Fisher-Problem anzuwenden.
Formulierung der Nullhypothese
Als Nullhypothese ist zu formulieren, dass die verkaufsfördernde Maßnahme 𝑌 durchschnittlich einen höheren Umsatz als Maßnahme 𝑋 erzielt, damit mit dem Ablehnen die Gegenhypothese, dass die verkaufsfördernde Maßnahme 𝑋 umsatzstärker als Maßnahme 𝑌 ist, als statistisch abgesichert angesehen werden kann:
Standardisierung der Prüfgröße/Teststatistik
Es gilt die Erwartungswerte voneinander abzuziehen und über die Varianz in die 𝑡-Verteilung zu standardisieren, wobei folgende Werte aus der Aufgabenstellung gelten:
𝑇 = 𝑃𝑟ü𝑓𝑔𝑟öß𝑒 ; 𝑋 ̅ = 45,75 ; 𝑌 ̅ = 35,25 ; 𝛿_0 = 0 ; 𝑆_𝑋^2 = 63,1 ; 𝑆_𝑦^2 = 115,4 ; 𝑁 = 4 ; 𝑀 = 4
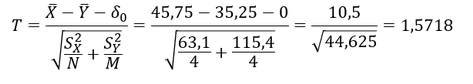
Ermittlung des kritischen Wertes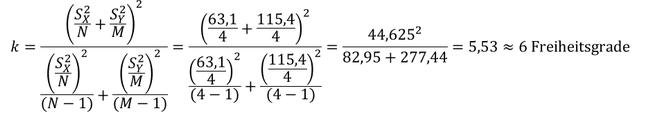
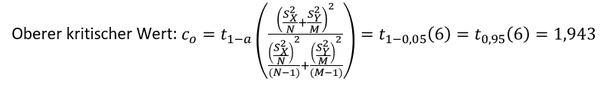
Es gilt den oberen kritischen Wert für das einseitige Testverfahren bei einem Signifikanzniveau von 𝛼 = 0,05 zu bestimmen. Da wir das Behrens-Fisher-Problem vorliegen haben, müssen wir allerdings zunächst bestimmen, unter welcher Anzahl an Freiheitsgraden 𝑘 wir in der 𝑡-Verteilung nachzuschlagen haben, mit 𝑁, 𝑀 = 4 und 𝑆_𝑥^2 = 63,1 bzw. 𝑆_𝑦^2 = 115,4:
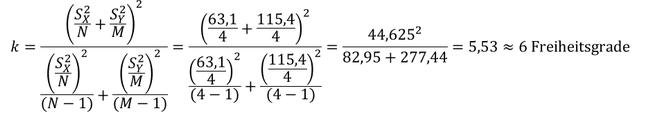
Der obere kritische Wert lässt sich nun mittels der 𝑡-Verteilung bestimmen, wobei das eigentlich 𝑁 mit dem Freiheitsgrad 𝑘 ersetzt wird:
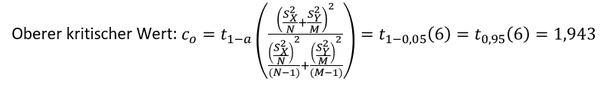
Merke: Der Freiheitsgrad sollte zunächst separat berechnet werden, damit der kritische Wert einfacher ermittelt werden kann. Zusätzlich kommt es häufig vor, dass der Freiheitsgrad 𝑘 bereits in der Aufgabenstellung angegeben ist, sodass eine Berechnung des Freiheitsgrades gar nicht notwendig ist.
Testentscheidung
Da die Prüfgröße kleiner als der obere kritische Wert ist, kann die Nullhypothese nicht abgelehnt werden:
𝑇 = 1,5718 < 𝑐_𝑜 = 1,943 ⇒ Nullhypothese nicht ablehnen/verwerfen
Es kann also nicht davon ausgegangen werden, dass die verkaufsfördernde Maßnahme 𝑋 zu einer weitaus größeren Umsatzsteigerung als die verkaufsfördernde Maßnahme 𝑌 führt.
Video "T-Differenztest":
Das Probe-Video behandelt die Thematik "T-Differenztest" des Kurses "Vertiefung der Statistik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Vertiefung Statistik-Paket
Übungen (optional)
18,5 h Lehrvideos
171 Skriptseiten
Formelsammlung
Klausurlösungen
Live-WebinareDas Vertiefung Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Vertiefung der Statistik" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 140 Übungsaufgaben, Übungsklausuren und zur Auffrischung statistischer Grundkenntnisse das "Grundlagen Statistik-Paket" zur Verfügung.
