Transponieren Matrix - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Lineare Algebra
Matrizen:
Bei Matrizen handelt es sich um mehrere in einer Tabelle zusammengefasste Vektoren, wobei auf Trennlinien verzichtet wird. Der Buchstabe 𝑚 bei einer Matrix drückt die Anzahl der Zeilenvektoren aus, 𝑛 hingegen die Anzahl der Spaltenvektoren.
Aufbau einer Matrix:
Matrizen werden durch einen fettgeschriebenen Großbuchstaben notiert. Bei der Buchstabenschreibweise der Zusammenfassung von Vektoren, erhält der Buchstabe den Index mn (𝑎_𝑚𝑛). Wie bereits erwähnt, steht der Buchstabe 𝑚 für den Zeilenvektor bzw. die Zeile, und 𝑛 für den Spaltenvektor bzw. die Spalte. 𝑎_23 würde in der Matrize also für die reelle Zahl in der 2. Zeile und der 3. Spalte stehen. So baut sich dann auch die Matrix auf:
In eine Matrix können beliebig viele Zeilen bzw. Spaltenvektoren aufgenommen werden. Vor die Matrix wird dann die Anzahl der Zeilen als auch Spalten geschrieben: (𝑚,𝑛)-Matrix
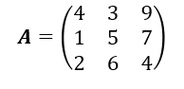
Beispiel einer (𝟑,𝟑)-Matrix:
Müssen sehr viele Rechenoperationen erfolgen, dient die Matrix als wesentlich übersichtlichere Schreibweise, als wenn man die Vektoren einzeln auflisten würde.
Transponieren einer Matrix:
Wie bei Vektoren lässt sich eine Matrix ebenfalls transponieren. Dabei wird der erste Zeilenvektor zum ersten Spaltenvektor umgeschrieben usw.. Die Transponierung wird ebenfalls durch ein hochgestelltes T oder ‘ gekennzeichnet.
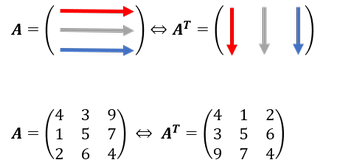
Transponierung einer Matrix:
Die Transponierung erfolgt, indem man den ersten Zeilenvektor als Spaltenvektor notiert, den zweiten Zeilenvektor als zweiten Spaltenvektor usw.
Transponierung einer nicht quadratischen Matrix: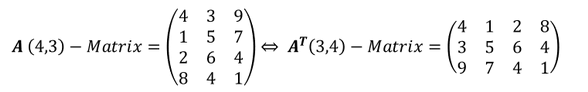
Transponiert man eine Matrix, in der die Reihen und Spalten nicht miteinander übereinstimmen, so tauscht man beim Transponieren die Reihenanzahl mit der Spaltenanzahl:
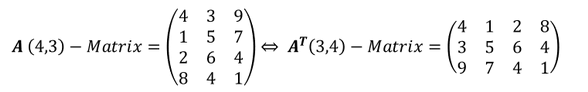
Durch das Transponieren einer Matrix kann die Anzahl der Zeilen und Spalten einer Matrix vertauscht werden!
Video "Transponieren Matrix":
Das Probe-Video behandelt die Thematik "Transponieren einer Matrix" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Addition und Subtraktion von Matrizen:
Bei der Addition und Subtraktion von Matrizen werden die einzelnen reellen Zahlen miteinander addiert bzw. subtrahiert. Sprich die oberste Zahl der einen Matrize wird mit der obersten Zahl der zweiten Matrize addiert oder subtrahiert usw.. Es können ausschließlich gleichdimensionierte Matrizen addiert werden, sprich bei denen Zeilen- und Spaltenanzahl übereinstimmen.
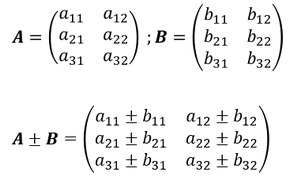
Beispiel:
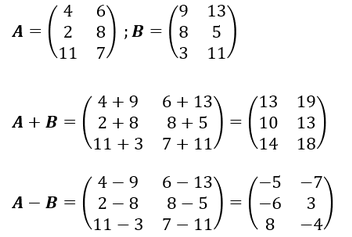
Multiplikation der Matrix mit einem Skalar (Matrix multipliziert mit einer Zahl):
Wird eine Matrix mit einer Zahl multipliziert, so ist jede reelle Zahl der Matrix mit dieser Zahl zu multiplizieren.
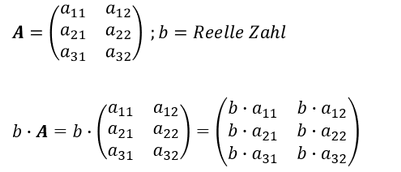
Beispiel: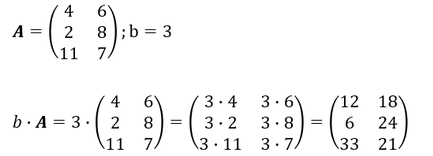
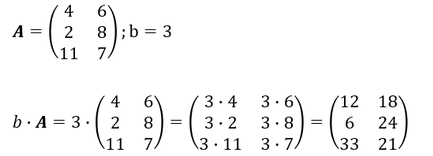
Grundlagen Wirtschaftsmathematik-Paket
21 h Lehrvideos
254 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
