Unterjährige Verzinsung - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Finanzmathematik
Unterjährige Verzinsung:
Erfolgt eine Zinszahlung nicht am Ende eines Jahres, so spricht man von einer unterjährigen Verzinsung. Dabei muss die Zinseszinsformel um die Anzahl der Zinsperioden 𝑚 erweitert werden. 𝑚 stellt dabei die Anzahl dar, wie viele Zinsauszahlungen innerhalb des Jahres stattfinden
Ermittlung der Anzahl der Zinsperioden:
Um die Anzahl der Zinsperioden 𝑚 zu ermitteln, lassen sich 2 Methoden voneinander unterscheiden, wobei es davon abgehängt, ob für die Zinszeitpunkte Monate oder Tage angegeben werden:
Anzahl der Zinsperioden bei Monatsverzinsungen:
Der Monatsintervall beschreibt dabei, nach wie vielen Monaten eine Zinszahlung stattfindet.
Würde beispielsweise monatlich verzinst werden, läge dieser bei 1, würde nur halbjährlich verzinst werden, läge dieser bei 6.
Anzahl der Zinsperioden bei Tagesverzinsungen:
Der Tageintervall beschreibt dabei, nach wie vielen Tagen eine Zinszahlung stattfindet.
Würde beispielsweise 15-tägig verzinst werden, läge dieser bei 15, würde nur 40-tägig verzinst werden, läge dieser bei 40.
!!! ACHTUNG !!!
Ob mit 360 oder 365 Tagen im Jahr gerechnet werden muss, sollte in der Aufgabe notiert sein
Endkapital bei unterjähriger Verzinsung:
Zur Errechnung des Endkapitals bei unterjähriger Verzinsung, muss die Zinseszinsformel wie folgt mit der Anzahl der Zinsperioden 𝑚 erweitert werden:
Beispiel: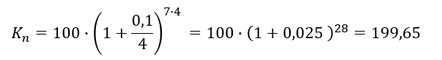 
Der Wert eines Sparbuchs beträgt zu Anfang 100€ (𝐾_0). Das Kapital wird zu einem Zinssatz von 10% p.a. (𝑖) angelegt. Die Verzinsung erfolgt quartalsweise (𝑚 = 12/3 = 4) über 7 Jahre (𝑛).
Welchen Endwert (𝐾_𝑛) hat das Sparbuch nach 7 Jahren?
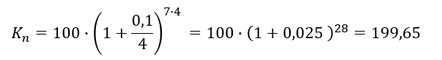
Video "Unterjährige Verzinsung":
Das Probe-Video behandelt die Thematik "Unterjährige Verzinsung" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Stetige Verzinsung:
Bei der stetigen Verzinsung sind die Zinsperioden unendlich kurz. Es wird sozusagen jede Nanosekunde das Kapital verzinst. Die Anzahl der Zinsperioden ist also unendlich (𝑚=∞)
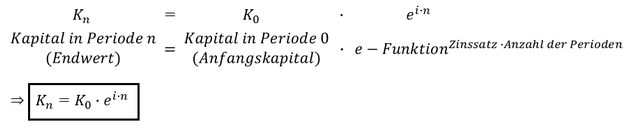
Formel zur Berechnung des Endwerts bei stetiger Verzinsung:
Der Endwert einer stetigen Verzinsung kann wie folgt errechnet werden:
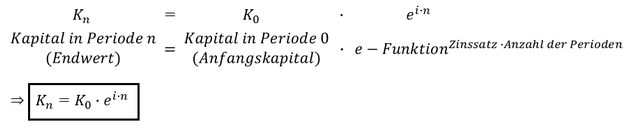
Beispiel: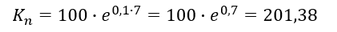 
Der Wert eines Sparbuchs beträgt zu Anfang 100€ (𝐾_0). Das Kapital wird stetig mit einem Zinssatz von 10% über 7 Jahre (𝑛) verzinst.
Welchen Endwert (𝐾_𝑛) hat das Sparbuch nach 7 Jahren?
Grundlagen Wirtschaftsmathematik-Paket
Live-Webinare
Übungen (optional)
21 h Lehrvideos
254 Skriptseiten
Formelsammlung
KlausurlösungenDas Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
