Unterschied Folge und Reihe - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Folgen und Reihen
Definition einer Folge:
Eine Zahlenfolge ist, wie der Name schon verrät, eine Folge von reellen Zahlen. Dafür wird jeder natürlichen Zahl eine reelle Zahl zugeordnet. Es wird zwischen einer endlichen und einer unendlichen Folge unterschieden. Ist der Folge eine definitive Zahl am Ende zugeordnet, handelt es sich um eine endliche Folge. Ist kein Ende zugeordnet, handelt es sich um eine unendliche Folge.
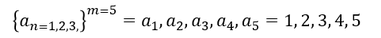
Endliche Folge:
Die endliche Folge bezeichnet man mit {𝒂_𝒏 }^𝒎, wobei n eine natürliche Zahl und m das Ende der Folge beschreibt.
Beispiel:
Unendliche Folge: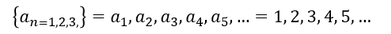
Die unendliche Folge bezeichnet man mit {𝒂_𝒏 }, wobei n eine natürliche Zahl darstellen soll und ein Ende nicht zugeordnet ist. Man könnte auch sagen: {𝑎_𝑛 }^∞.
Beispiel:
Definition einer Reihe:
Eine Reihe stellt die Aufsummierung der einzelnen Folgenglieder dar. Ein Folgenglied ist dabei die einzelne Zahl einer Folge. Es kann zwischen einer endlichen und unendlichen Reihe unterschieden werden. Handelt es sich um eine endliche Folge, so ist auch die Reihe endlich. Handelt es sich um eine unendliche Folge, so ist auch die Reihe unendlich.
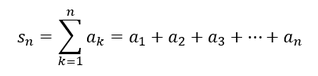
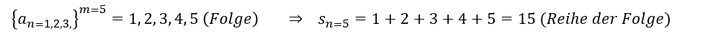
Endliche Reihe:
Die endliche Reihe bezeichnet man mit 𝒔_𝒏, wobei n das Ende der Reihe beschreibt:
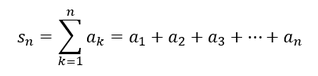
Beispiel:
Unendliche Reihe:
Die unendliche Reihe bezeichnet man mit 𝒔_(𝒏 = ∞), wobei 𝒏=∞ die Unendlichkeit der Reihe beschreibt: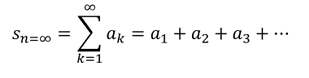
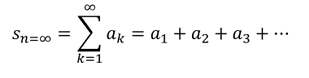
Beispiel: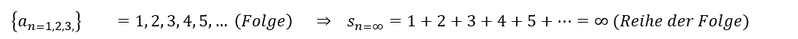
Video "Unterschied Folge und Reihe":
Das Probe-Video behandelt die Thematik "Unterschied von Folgen und Reihen" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Monoton wachsende Folge:
Jedes Folgenglied ist größer oder gleich dem vorherigen Folgenglied: 𝒂_(𝒏+𝟏) ≥ 𝒂_𝒏
Beispiel:
𝑎_𝑛 = 1, 2, 2, 3, 3, 4, 5 ; 𝑎_𝑛 = 1, 2, 3, 4, 5, 6, 7
Streng monoton wachsende Folge:
Jedes Folgenglied ist größer dem vorherigen Folgenglied: 𝒂_(𝒏+𝟏) > 𝒂_𝒏
Beispiel:
𝑎_𝑛 = 1, 2, 3, 4, 5, 6, 7 ; 𝑎_𝑛 = 1 , 1,5 , 2 , 2,5 , 3
Streng monoton wachsende Folgen sind gleichzeitig immer monoton wachsend!
Grafisch:
Tipp: Um die Monotonie einer Folge leichter bestimmen zu können, müssen die Folgeglieder nur durch Linien verbunden werden:
Keine Monotonie: Linie steigt und fällt in einem oder mehreren Punkten
Monoton wachsend: Linie steigt und ist in einem oder mehreren Punkten waagerecht
Streng monoton wachsend: Linie steigt in allen Punkten
Monoton fallende Folge:
Jedes Folgenglied ist kleiner oder gleich dem vorherigen Folgenglied: 𝒂_(𝒏+𝟏) ≤ 𝒂_𝒏
Beispiel:
𝑎_𝑛 = 7, 6, 6, 5, 4, 4, 3 ; 𝑎_𝑛 = 7, 6, 5, 4, 3, 2, 1
Streng monoton fallende Folge:
Jedes Folgenglied ist kleiner dem vorherigen Folgenglied: 𝒂_(𝒏+𝟏) < 𝒂_𝒏
Beispiel:
𝑎_𝑛 = 7, 6, 5, 4, 3, 2, 1 ; 𝑎_𝑛 = 3, 2,5, 2, 1,5, 1
Streng monoton fallende Folgen sind gleichzeitig immer monoton fallend!
Grafisch:
Tipp: Um die Monotonie einer Folge leichter bestimmen zu können, müssen die Folgeglieder nur durch Linien verbunden werden:
Keine Monotonie: Linie fällt und steigt in einem oder mehreren Punkten
Monoton fallend: Linie fällt und ist in einem oder mehreren Punkten waagerecht
Streng monoton fallend: Linie fällt in allen Punkten
Grundlagen Wirtschaftsmathematik-Paket
21 h Lehrvideos
254 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
