Varianzzerlegung - Vertiefung der Statistik - Fernuni Hagen
Vertiefung Statistik-Paket > Vertiefung-Statistik > Regressionsanalyse
Grundlage der Varianz-Zerlegung mit Hilfe eines Beispiels:
Das lineare Regressionsmodell dient dazu, mit Hilfe der Vorgabe eines Wertes des Merkmals 𝑋, die Prognose bzw. die Schätzung des Wertes des abhängigen Merkmals 𝑌 zu verbessern, sofern ein gewisser linearer Zusammenhang zwischen beiden Merkmalen besteht. Nehmen wir beispielsweise einen gewissen linearen Zusammenhang zwischen Temperatur und Anzahl der Sonnenstunden am Tag an, so können wir mit Hilfe der geschätzten Regressionsgeraden aus dem Datenmaterial für eine vorgegebene Temperatur die Anzahl der Sonnenstunden am Tag besser einschätzen. Sollen wir hingegen ohne weiteres Merkmal die Sonnenstunden für einen Tag schätzen, so bliebe uns nichts anderes übrig als den Mittelwert als zuverlässigsten Schätzwert unseres Datenmaterials anzunehmen. Die folgende Grafik soll das Beispiel nochmal verdeutlichen:
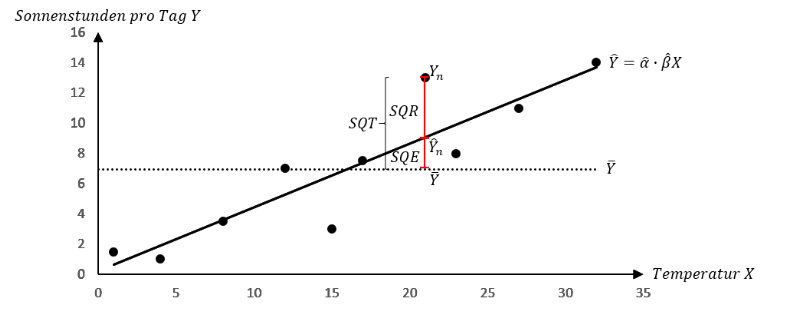
Es lässt sich erkennen, dass die beobachteten Werte 𝑋,𝑌 (als Punkte dargestellt) besser durch die Regressionsgerade, als durch den Mittelwert geschätzt werden können bzw. in der Summe die Streuung um die Regressionsgerade geringer ist, als die Streuung um den Mittelwert. Das Regressionsmodell erklärt also, mit Hilfe des linearen Zusammenhangs von 𝑋 und 𝑌, die Streuung um den Mittelwert in der Hinsicht, dass bei niedrigen Temperaturen die Sonnenstunden pro Tag nach unten abweichen und bei hohen Temperaturen die Sonnenstunden nach oben abweichen.
Die Abweichungen der Prognosewerte 𝑌 ̂_𝑛 der Regressionsgeraden vom Mittelwert 𝑌 ̅ erklären also die Abweichungen des beobachteten Wertes 𝑌_𝑛 vom Mittelwert 𝑌 ̅ zu einem bestimmten Maß und ermöglichen so eine Zerlegung der Gesamtvarianz bzw. Gesamtstreuung (𝑆𝑄𝑇) in eine erklärte Streuung (𝑆𝑄𝐸) und eine Reststreuung (𝑆𝑄𝑅):
Totale Streuung: 𝑆𝑄𝑇 = ∑_𝑛 (𝑌_𝑛 − 𝑌 ̅ )^2 (Die Summe der quadrierten Abweichung der beobachteten Werte 𝑌_𝑛 vom Mittelwert 𝑌 ̅ stellt die Gesamtstreuung dar.)
Erklärte Streuung: 𝑆𝑄𝐸 = ∑_𝑛 (𝑌 ̂_𝑛 − 𝑌 ̅ )^2 (Die Summe der quadrierten Abweichung der Prognosewerte 𝑌 ̂_𝑛 vom Mittelwert 𝑌 ̅ stellt die erklärte Streuung dar.)
Rest-Streuung: 𝑆𝑄𝑅 = ∑_𝑛 (𝑌_𝑛 − 𝑌 ̂_𝑛 )^2 (Die Summe der quadrierten Abweichung der beobachteten Werte 𝑌_𝑛 von den Prognosewerten 𝑌 ̂_𝑛 stellt die Reststreuung dar.)
Merke: Bei der Rest-Streuung handelt es sich um die Restabweichung des Beobachtungswertes vom Mittelwert, die auch das lineare Regressionsmodell mit Hilfe seiner Abweichung der Prognosen vom Mittelwert nicht erklären kann.
Video "Varianzzerlegung":
Das Probe-Video behandelt die Thematik "Varianzzerlegung" des Kurses "Vertiefung der Statistik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Allgemeine Berechnung der Streuungen der Varianz-Zerlegung:
Für die Varianz-Zerlegung gilt allgemein, dass die Totalstreuung 𝑆𝑄𝑇 in die erklärte Streuung 𝑆𝑄𝐸 und die Reststreuung 𝑆𝑄𝑅 zerlegt wird. Die Streuungen weisen dabei folgende mathematische Zusammenhänge und Methoden zur Berechnung der einzelnen Streuungen auf:
Mathematischer Zusammenhang der Varianz-Zerlegung:
Die Totalstreuung setzt sich zusammen aus der erklärten Streuung 𝑆𝑄𝐸 und der Reststreuung 𝑆𝑄𝑅:
𝑆𝑄𝑇 = 𝑆𝑄𝐸 + 𝑆𝑄𝑅
Berechnung der Totalstreuung 𝑺𝑸𝑻
Die Totalstreuung lässt sich mit Hilfe der Varianz von 𝑌 (𝑆_𝑦^2 ) und dem Stichprobenumfang 𝑁 berechnen, sofern diese Werte bekannt sind. Denn es gilt:
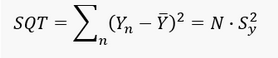
Berechnung der erklärten Streuung 𝑺𝑸𝑬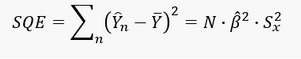
Die erklärte Streuung lässt sich mit Hilfe des geschätzten Parameters 𝛽 ̂, der Varianz von 𝑋 (𝑆_𝑥^2 ) und dem Stichprobenumfang 𝑁 berechnen, sofern diese Werte bekannt sind. Denn es gilt:
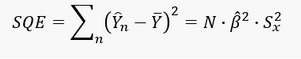
Berechnung der Reststreuung 𝑺𝑸𝑹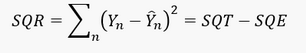
Die Reststreuung lässt sich mit Hilfe des Wissens über die Werte der Totalstreuung 𝑆𝑄𝑇 und der erklärten Streuung 𝑆𝑄𝐸 berechnen:
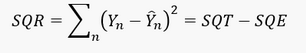
Merke: Mit Hilfe der Reststreuung lässt sich der Varianz-Schätzer der Regressionsgeraden ermitteln, wobei die Reststreuung aufgrund der Berücksichtigung von Freiheitsgraden noch durch 𝑁 − 2 zu teilen ist, damit sich ein erwartungstreuer Schätzer ergibt. So gelangen wir zu der bekannten Formel für den Varianz-Schätzer der Regressionsgeraden:
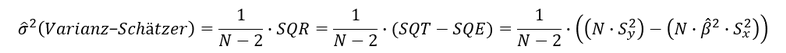
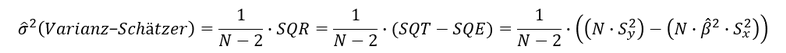
Vertiefung Statistik-Paket
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)
18,5 h Lehrvideos
171 SkriptseitenDas Vertiefung Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Vertiefung der Statistik" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 140 Übungsaufgaben, Übungsklausuren und zur Auffrischung statistischer Grundkenntnisse das "Grundlagen Statistik-Paket" zur Verfügung.
