Wilcoxon-Rangsummen-Test - Vertiefung der Statistik - Fernuni Hagen
Vertiefung Statistik-Paket > Vertiefung-Statistik > Zweistichproben-Testverfahren
Beispielhafte Aufgabe für den Wilcoxon-Rangsummen-Test:
Ein Unternehmen betreibt zwei verschiedene verkaufsfördernde Maßnahmen 𝑋 und 𝑌. Anhand der Umsatzsteigerungen möchte das Unternehmen die Maßnahmen vergleichen, wobei es davon ausgeht, dass beide Maßnahmen die gleiche Umsatzsteigerung erzielen. Eine Verteilungsannahme über das Datenmaterial wird nicht getroffen. Es liegen folgende Daten bezüglich der Umsatzsteigerungen vor:
Wie lautet die passende Nullhypothese für das statistische Testverfahren und kann die Nullhypothese bei einem Signifikanzniveau von 𝛼=0,1 abgelehnt werden?
Wie lauten neben der Testentscheidung der Erwartungswert und die Varianz der Prüfgröße?
Lösung Wilcoxon-Rangsummen-Test :
Wahl des Testverfahrens
Es sollen die ermittelten Umsatzsteigerungen miteinander verglichen werden. Da keine Verteilungsannahme getroffen wird und 𝑁,𝑀<25 ist, ist der Wilcoxon-Rangsummen-Test zu verwenden.
Formulierung der Nullhypothese
Als Nullhypothese ist zu formulieren, dass die verkaufsfördernden Maßnahme 𝑋 und 𝑌 im Mittel die gleiche Umsatzsteigerung erzielen, damit mit dem Ablehnen die Gegenhypothese, dass die verkaufsfördernden Maßnahmen im Mittel nicht gleich sind, als statistisch abgesichert angesehen werden kann:
Standardisierung der Prüfgröße/Teststatistik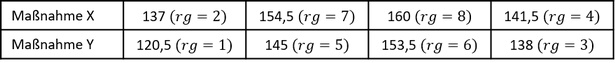
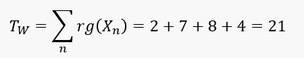
Es gilt die Daten als gepoolte Stichprobe zu betrachten und den Werten aufsteigend eindeutige Ränge zuzuordnen. Die Prüfgröße 𝑇_𝑊 ergibt sich als Summe der Ränge von 𝑋:
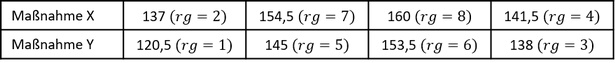
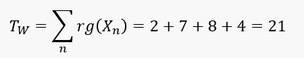
Merke: Im Falle von Bindungen sind Durchschnittsränge zu bilden.
Ermittlung der kritischen Werte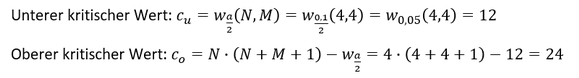
Es gilt den unteren und oberen kritischen Wert für das zweiseitige Testverfahren bei einem Signifikanzniveau von 𝛼=0,1 mittels der Wilcoxon-Rangsummen-Tabelle zu bestimmen. Dabei lässt sich der obere kritische Wert nur mit Hilfe des unteren kritischen Wertes bestimmen:
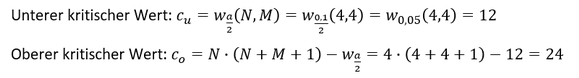
Testentscheidung
Da die Prüfgröße größer als der untere kritische Wert, aber kleiner als der obere kritische Wert ist, kann die Nullhypothese nicht abgelehnt werden:
Video "Wilcoxon-Rangsummen-Test":
Das Probe-Video behandelt die Thematik "Wilcoxon-Rangsummen-Test" des Kurses "Vertiefung der Statistik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Erwartungswert und Varianz der Prüfgröße/Teststatistik
Beim Wilcoxon-Testverfahren lässt sich für die Prüfgröße/Teststatistik eigens ein Erwartungswert und eine Varianz berechnen, da die Prüfgröße eines Wilcoxon-Testverfahrens allein anhand von Rängen bestimmt wird. Entsprechend sind die beiden Parameter Erwartungswert und Varianz der Prüfgröße 𝑇_𝑊 vom Stichprobenumfang 𝑁 bzw. 𝑀 abhängig und lassen sich wie folgt berechnen:
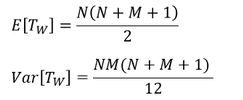
Für den Erwartungswert und die Varianz der Prüfgröße 𝑇_𝑊 für das angegebene Beispiel mit 𝑁=4 und 𝑀=4 gilt entsprechend:
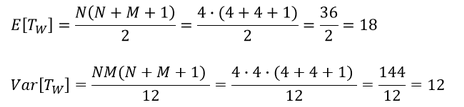
Merke: Die Formeln zur Berechnung des Erwartungswertes und der Varianz der Prüfgröße des Wilcoxon-Rangsummen-Testverfahrens lassen sich in der Kurseinheit auf der gegenüberliegenden Seite mit der ersten Quantil-Tabelle finden.
Vertiefung Statistik-Paket
Übungen (optional)
18,5 h Lehrvideos
171 Skriptseiten
Formelsammlung
Klausurlösungen
Live-WebinareDas Vertiefung Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Vertiefung der Statistik" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 140 Übungsaufgaben, Übungsklausuren und zur Auffrischung statistischer Grundkenntnisse das "Grundlagen Statistik-Paket" zur Verfügung.
