Zinseszinsrechnung - Grundlagen der Wirtschaftsmathematik - Fernuni Hagen
Grundlagen Wirtschaftsmathemaitk-Paket > Grundlagen-Wirtschaftsmathematik > Finanzmathematik
Verzinsung bei einer Periode:
Bei der Verzinsung einer Periode wird das Kapital zum Kapitalmarktzins (Zinssatz) über eine Periode angelegt und vermehrt.
Angenommene Ausgangssituation:
Auf einem Sparbuch liegen 100€, welche mit 10% pro Periode (bsp. jährlich) verzinst werden. Wie hoch ist der Wert des Sparbuchs nach einer Periode?
Berechnung der Ausgangssituation:
Zur Errechnung der Zinsen für eine Periode muss das Kapital mit dem Zinssatz multipliziert werden:
Um den Wert des Sparbuchs nach einer Periode zu errechnen, müssen die Zinsen dem Kapital hinzuaddiert werden:
Diese Methode hat 2 Rechenschritte zur Folge und ist sehr umständlich. Die Errechnung des Kapitals in Periode 1 kann wesentlich leichter in einem Schritt erfolgen.
Verzinsung einer Periode mit einem Schritt:
Statt das Kapital mit 10% zu verzinsen und die Zinsen in einem 2. Schritt wieder zum Kapital hinzuzuaddieren, kann man dies auch in einem Schritt realisieren, indem man, statt das Kapital mit 10% zu verzinsen, dieses mit 110% verzinst, sodass das Kapital vom Zeitpunkt 0 mit 100% vertreten bleibt.
Das führt zu folgendem mathematischen Zusammenhang:
Berechnung der Ausgangssituation: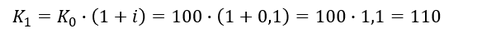
Unterstellen wir wieder die Ausgangsituation von 100€ (𝐾_0) und 10% (𝑖) Verzinsung für eine Periode ergibt sich der Wert:
Wir kommen zum gleichen Ergebnis. Allerdings gilt diese Formel nur für eine Periode.
Video "Zinseszinsrechnung":
Das Probe-Video behandelt die Thematik "Zinseszinsrechnung" des Kurses "Grundlagen der Wirtschaftsmathematik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Einfache Verzinsung:
Bei der einfachen Verzinsung müssen keine Zinseszinsen berücksichtigt werden. Es wird davon ausgegangen, dass die Zinsen in jeder Periode gleich sind und der ersten Periode entsprechen.
Angenommene Ausgangssituation:
Auf einem Sparbuch liegen 100€, welche mit 10% pro Periode (bsp. jährlich) verzinst werden. Wie hoch ist der Wert des Sparbuchs nach sieben Perioden?
Berechnung der Ausgangssituation:
Wir wissen, dass die Zinsen der ersten Periode 10€ entsprechen. Da keine Zinseszinsen zu berücksichtigen sind, können wir einfach die 10€ mit 7 multiplizieren:
𝐾_7 = 100 + 10 ∙ 7 = 170
Nach 7 Perioden der einfach Verzinsung wäre das Sparbuch 170€ Wert. Dies entspräche dem Grunde nach einer Verzinsung von 70%.
Mathematische Berechnung der einfachen Verzinsung mehrerer Perioden:
Die einfache Verzinsung lässt sich für beliebig viele Perioden (𝑛) einfach in unsere Formel einbauen, indem der Zinssatz mit der Anzahl der Perioden multipliziert wird:
Setzen wir nun unsere Ausgangssituation in die Formel ein:
𝐾_(𝑛 = 7) = 𝐾_0 ∙ (1 + 𝑛 ∙ 𝑖) = 100 ∙ (1 + 7 ∙ 0,1) = 100 ∙ (1 + 0,7) = 100 ∙ 1,7 𝑏𝑧𝑤. 100 ∙ 170% = 170
𝐾_7 = 170
Die einfache Verzinsung ist relativ leicht zu errechnen, allerdings werden hier die Zinseszinsen vernachlässigt, weshalb die einfache Verzinsung selten angewandt wird.
!!!ACHTUNG !!!
Spricht man in der Betriebswirtschaftslehre von Verzinsung, wird sofort davon ausgegangen, dass die Zinseszinsen mitberücksichtigt werden!
Zinseszinsrechnung:
Bei der Zinseszinsrechnung finden auch die auf die Zinsen pro Periode anfallenden Zinsen Berücksichtigung.
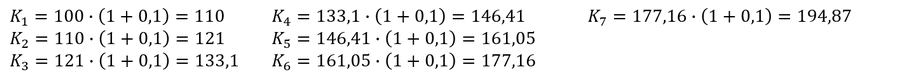
Angenommene Ausgangssituation:
Auf einem Sparbuch liegen 100€, welche mit 10% pro Periode (bsp. jährlich) verzinst werden. Wie hoch ist der Wert des Sparbuchs nach sieben Perioden?
Berechnung der Ausgangssituation:
Um die Zinseszinsen zu berücksichtigen, muss der Wert des Sparbuchs nach jeder Periode erneut verzinst werden:
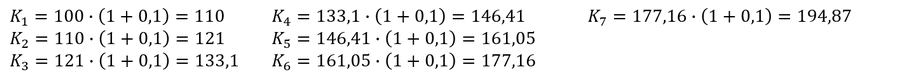
So viele Rechenschritte wären viel zu umständlich. Wir könnten auch direkt immer erneut multiplizieren, ohne den Schritt des Ergebnisses:
𝐾_7 = 100 ∙ (1 + 0,1) ∙ (1 + 0,1) ∙ (1 + 0,1) ∙ (1 + 0,1) ∙ (1 + 0,1) ∙ (1 + 0,1) = 194,87
Auch das wäre zu umständlich. Da wir 7x immer das Gleiche multiplizieren, können wir auch einfach „Hoch 7“ verwenden:
𝐾_7 = 100 ∙ (1 + 0,1)^7 = 194,87
Mathematische Berechnung der Zinseszinsrechnung:
Für die Zinseszinsrechnung kommen wir somit zu folgender Formel:
Grundlagen Wirtschaftsmathematik-Paket
21 h Lehrvideos
254 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Grundlagen Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Grundlagen der Analysis und Linearen Algebra" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen mathematischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 150 Übungsaufgaben und Übungsklausuren zur Verfügung.
