Bedingte Verteilung - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Zweidimensionale Häufigkeitsverteilung
Grundlage der bedingten/konditionalen Verteilung:
Die bedingte Verteilung, welche auch konditionale Verteilung genannt wird, gibt die Häufigkeitsverteilung eines Merkmals unter der Voraussetzung, dass für das andere Merkmal eine bestimmte Merkmalsausprägung gilt, wieder. Bedingte Verteilungen werden meist dann gebraucht, wenn die Verteilung eines Merkmals unter einer bestimmten Voraussetzung des anderen Merkmals von Interesse ist. Beispielsweise ist die Verteilung des Merkmals Familienstand (ledig, verheiratet, geschieden, verwitwet) nur bei dem Geschlecht „weiblich“ von Interesse. Mit der bedingten Verteilung kann sich also auf eine bestimmte Merkmalsausprägung (𝑦_𝑘 oder 𝑥_𝑗) fokussiert werden und die Verteilung des anderen Merkmals (𝑋 oder 𝑌) unter Voraussetzung dieser Merkmalsausprägung betrachtet werden.
Berechnung der bedingten/konditionalen Verteilung:
Die bedingte Verteilung bezieht sich im eigentlichen Sinne nur auf die relativen Häufigkeiten, da die bedingte Verteilung zu keinerlei Veränderungen der absoluten Häufigkeiten führt. Die bedingten absoluten Häufigkeiten lassen sich einfach in der Spalte/Zeile der vorgegebenen Merkmalsausprägung ablesen. Um zu den bedingten relativen Häufigkeiten zu gelangen, bedarf es allerdings einer Berechnung, wobei zu unterscheiden ist, ob die bedingte Verteilung für das Merkmal 𝑋 unter Voraussetzung einer Merkmalsausprägung 𝑦_𝑘 oder die bedingte Verteilung des Merkmals 𝑌 für ein vorausgesetztes 𝑥_𝑗 betrachtet werden soll.
Bedingte/konditionale Verteilung für Merkmal 𝑿: Soll die Verteilung des Merkmals 𝑋 unter der Annahme einer bestimmten Merkmalsausprägung des Merkmals 𝑌 (𝑦_𝑘) betrachtet werden, wird für die bedingte Verteilung einer Merkmalskombination die Notation 𝑓(𝑥_𝑗│𝑦_𝑘 ) verwendet. Zur Berechnung der bedingten Verteilung einer Merkmalskombination, ist die Häufigkeit der Merkmalskombination ℎ(𝑥_𝑗,𝑦_𝑘) / 𝑓(𝑥_𝑗,𝑦_𝑘) durch die Häufigkeit der vorgegebenen Merkmalsausprägung h(𝑦_𝑘 ) / 𝑓(𝑦_𝑘) zu dividieren:
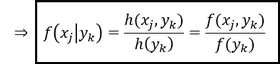
Bedingte/konditionale Verteilung für Merkmal 𝒀: Soll die Verteilung des Merkmals 𝑌 unter der Annahme einer bestimmten Merkmalsausprägung des Merkmals 𝑋 (𝑥_𝑗) betrachtet werden, wird für die bedingte Verteilung einer Merkmalskombination die Notation 𝑓(𝑦_𝑘│𝑥_𝑗 ) verwendet. Zur Berechnung der bedingten Verteilung einer Merkmalskombination, ist die Häufigkeit der Merkmalskombination ℎ(𝑥_𝑗,𝑦_𝑘) / 𝑓(𝑥_𝑗,𝑦_𝑘) durch die Häufigkeit der vorgegebenen Merkmalsausprägung h(𝑥_𝑗 ) / 𝑓(𝑥_𝑗) zu dividieren: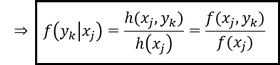
Merke: Zur Berechnung der bedingten relativen Häufigkeit einer Merkmalskombination ist die Häufigkeit der Merkmalskombination lediglich durch die Randverteilung der vorgegebenen Merkmalsausprägung zu dividieren, welche als zweites genannt wird.
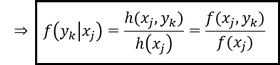
Merke: Zur Berechnung der bedingten relativen Häufigkeit einer Merkmalskombination ist die Häufigkeit der Merkmalskombination lediglich durch die Randverteilung der vorgegebenen Merkmalsausprägung zu dividieren, welche als zweites genannt wird.
Video "Bedingte Verteilung":
Das Probe-Video behandelt die Thematik "Bedingte Verteilung" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Beispielhafte Bestimmungen verschiedener bedingter/konditionaler Verteilungen anhand einer Häufigkeitstabelle zweier Merkmale:
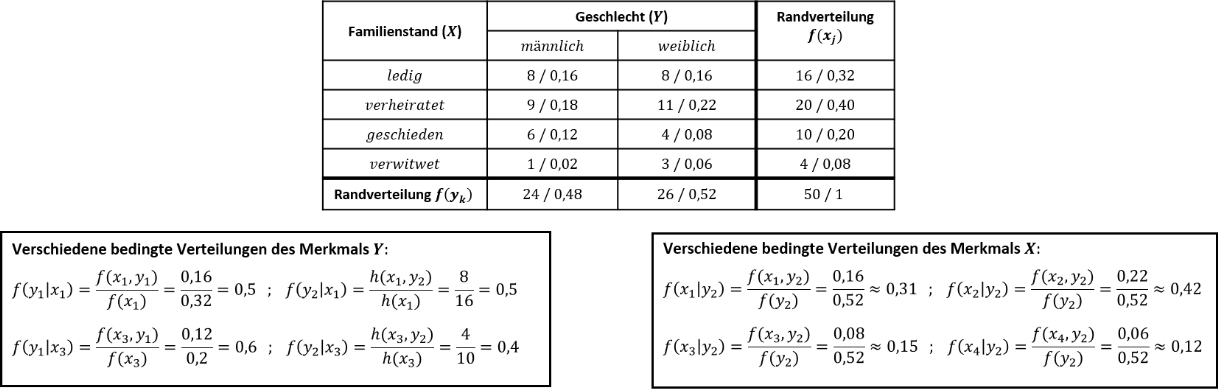
Zum besseren Verständnis der bedingten/konditionalen Verteilung wollen wir im Folgenden von dem bekannten Geschlecht/Familienstand Beispiel ausgehen, in welchem das Geschlecht und der Familienstand von 𝑛 = 50 Personen erhoben wurde. Es sollen bestimmte bedingte Häufigkeitswerte anhand der angegebenen Kontingenztabelle der absoluten/relativen Häufigkeiten bestimmt werden:
Aussagekraft der bedingten/konditionalen Verteilung:
Mittels der bedingten/konditionalen Verteilungen können Aussagen über die Verteilungen der Merkmale unter der vorgegebenen Merkmalsausprägung getroffen werden:
- 𝑓(𝑦_1│𝑥_1 ) und 𝑓(𝑦_2│𝑥_1 ): Die Personen, welche als Familienstand „ledig“ angegeben haben, sind zur Hälfte (50%) Männer und zur Hälfte (50%) Frauen.
- 𝑓(𝑦_1│𝑥_3 ) und 𝑓(𝑦_2│𝑥_3 ): Die Personen, welche als Familienstand „geschieden“ angegeben haben, sind zu 60% Männer und nur zu 40% Frauen.
- 𝑓(𝑥_1│𝑦_2 ) , 𝑓(𝑥_2│𝑦_2 ), 𝑓(𝑥_3│𝑦_2 ) , 𝑓(𝑥_4│𝑦_2 ): Unter allen befragten Frauen sind 31% ledig, 42% verheiratet, 15% geschieden und 12% verwitwet.
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


