Chi-Quadrat Anpassungstest - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Statistische Testverfahren
𝝌^𝟐-Anpassungstest:
Der 𝜒^2-Anpassungstest ermöglicht die Prüfung einer Nullhypothese, welche eine Aussage über die Verteilung einer Grundgesamtheit trifft. Der Anpassungstest kann dabei sowohl für alle möglichen Skalierungen (nominal-, ordinal-, metrisch skaliert) als auch für alle Abzählbarkeiten (diskret/stetig) eines Merkmals der Grundgesamtheit erfolgen. Bei der Erhebung der Stichprobe steht nicht mehr die Schätzung über einen Parameter im Vordergrund, sondern die Häufigkeiten, wie oft bestimmte Realisationen bei der Stichprobenerhebung aufgetreten sind. Die Häufigkeitswerte der Realisationen aus der Stichprobe werden dann mit den Häufigkeiten verglichen, die bei der unterstellten Verteilung der Nullhypothese eigentlich hätten auftreten müssen. Stellt sich heraus, dass die Abweichungen sehr groß sind, gilt es, die Nullhypothese abzulehnen.
Merke: Zur Abbildung der Häufigkeiten von stetigen Merkmalen oder vielen möglichen Ausprägungen sind Klassen (Gruppen) zu bilden.
Nullhypothese des 𝝌^𝟐-Anpassungstests:
Die Nullhypothese des 𝜒^2-Anpassungstests trifft eine Aussage über die Verteilung der Grundgesamtheit. Dabei wird die angenommene Verteilung als Nullhypothese formuliert, sodass mit dem Ablehnen der Nullhypothese das Gegenteil, dass die Grundgesamtheit nicht wie angenommen verteilt ist, statistisch nachgewiesen wird. Die Angabe der Verteilung in der Nullhypothese erfolgt dabei über die Anteilswerte 𝜋_𝑗, die die Verteilungsverhältnisse bzw., bei Multiplikation mit der Anzahl 𝑛, die Häufigkeitsverhältnisse der möglichen Realisationen/Klassen angeben. Meist kann dabei zwischen folgenden zwei unterstellten Verteilungsmöglichkeiten unterschieden werden:
Gleichverteilung: Jede Realisation/Klasse tritt mit dem gleichen Anteil 𝜋_𝑗 bzw. mit der gleichen Häufigkeit 𝑛 ∙ 𝜋_𝑗 auf.
Verhältnisverteilung: Jede Realisation/Klasse steht in einem bestimmten Anteilsverhältnis 𝜋_𝑗 bzw. in einem bestimmten Häufigkeitsverhältnis 𝑛 ∙ 𝜋_𝑗 zueinander.
Beispiele:
Gleichverteilung: Die möglichen Realisationen eines Würfels (1,2,3,4,5,6) sind gleichverteilt mit einem Anteil von 𝜋_𝑗 = 1/6 bzw. bei beispielsweise 𝑛 = 12 Würfen mit einer gleichen Häufigkeit aller Realisationen von 𝑛 ∙ 𝜋_𝑗 = 12 ∙ 1/6 = 2.
Verhältnisverteilung: Die Zutaten Butter, Mehl, Zucker (Realisationen) stehen in einem Verhältnis von 1:3:2 zueinander, wobei für die Anteilswerte gilt 𝜋_1 = 1/6 ; 𝜋_2 = 3/6 ; 𝜋_3 = 2/6 bzw. bei beispielsweise 𝑛 = 1200 Gramm mit den Häufigkeiten 𝑛𝜋_1 = 1200 ∙ 1/6 = 200𝑔 Butter, 𝑛𝜋_2 = 1200 ∙ 3/6 = 600𝑔 Mehl und 𝑛𝜋_3 = 1200 ∙ 2/6 = 400𝑔 Zucker.
Notwendige Angaben des 𝝌^𝟐-Anpassungstests:
Neben der vermuteten Verteilungsangabe über die Grundgesamtheit, bedarf es über das Wissen der auftretenden Häufigkeiten ℎ_𝑗 der möglichen Realisationen/Klassen 𝑗 bei der Stichprobe eines Merkmals. So kann in der Prüfung schnell erkannt werden, wann ein 𝜒^2-Anpassungstest durchgeführt werden muss, wobei die Häufigkeiten ℎ_𝑗 meist in Tabellenform angegeben werden:

Allgemeine Durchführung des 𝛘^𝟐-Anpassungstests:
Zur allgemeinen Prüfung, ob die Nullhypothese über die Verteilung einer Grundgesamtheit abzulehnen ist, bedarf es einer Prüfgröße und eines kritischen Wertes bzw. einer Grenze, die den Ablehnungsbereich definieren. Als Prüfgröße des Anpassungstests dient dabei die 𝜒^2-Verteilung, wobei der Vergleich der Häufigkeiten der Stichprobe mit den Häufigkeiten der unterstellten Verteilung durch eine mathematisch Berechnung in einen passenden Wert der 𝜒^2-Verteilung überführt werden kann. Eine Grenze für den Ablehnungsbereich lässt sich dann mittels der angegebenen Irrtumswahrscheinlichkeit 𝛼 in der 𝜒^2-Verteilung finden.
Mathematische Ermittlung der Prüfgröße des 𝝌^𝟐-Anpassungstests:
Die in der Stichprobe auftretenden Häufigkeiten der möglichen Realisationen/Klassen werden mit ℎ_𝑗 notiert. Die Häufigkeiten, die sich nach der unterstellten Verteilung der Nullhypothese ergeben sollten, lassen sich durch Multiplikation der Anteilswerte 𝜋_𝑗 mit dem Umfang der Stichprobe 𝑛 ermitteln (𝜋_𝑗 ∙ 𝑛). Die mathematische 𝜒^2-Prüfgröße ergibt sich dann durch die Summe der jeweiligen Häufigkeiten der Stichprobe abzüglich der jeweiligen Häufigkeit bei unterstellter Verteilung zum Quadrat, dividiert durch die jeweilige Häufigkeit der unterstellten Verteilung:
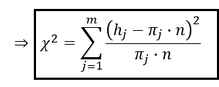
Merke: Durch die Multiplikation der angegebenen Anteilswerte 𝜋_𝑗 der Nullhypothese mit dem Stichprobenumfang 𝑛, lassen sich die Häufigkeiten ermitteln, wie oft die Realisation/Klasse unter der unterstellten Verteilung auftreten müsste.
Ermittlung des kritischen Wertes/der Grenze des 𝝌^𝟐-Anpassungstests:
Der 𝜒^2-Anpassungstest weist nur eine obere Grenze auf. Sobald diese überschritten wird, ist die Abweichung der Häufigkeiten der Stichprobe von der unterstellten Verteilung so groß, dass die Nullhypothese abzulehnen ist. Die obere Grenze befindet sich in der Chi-Quadrat-Verteilung bei der Wahrscheinlichkeit 1 − 𝛼 bei 𝑚 − 1 Freiheitsgraden. Für die obere Grenze bzw. den Nicht-Ablehnungs-/Ablehnungsbereich mit der Irrtumswahrscheinlichkeit 𝛼 gilt folglich:
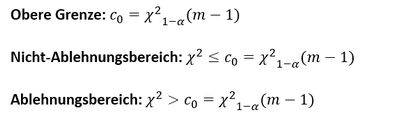
ACHTUNG: Die Freiheitsgrade werden mittels 𝑚, der Anzahl der möglichen Realisationen/Anzahl der Klassen und nicht mittels des Stichprobenumfangs 𝑛 bestimmt!
Video "Chi-Quadrat Anpassungstest":
Das Probe-Video behandelt die Thematik "Chi-Quadrat Anpassungstest" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Anwendungsbeispiele des 𝝌^𝟐-Anpassungstests:
Um die Vorgehensweise bei der Durchführung des 𝜒^2-Anpassungstests besser verdeutlichen zu können, wollen wir zwei Beispiele berechnen.
Beispiel 1:
Es soll geprüft werden, ob die Umsätze des Unternehmens an den verschiedenen Wochentagen gleich hoch sind. Aus einer Stichprobe wurde folgende Verteilung der Umsätze nach Wochentagen ermittelt:

Es ist die Hypothese zu prüfen, dass der Umsatz für alle Wochentage gleich hoch ist, bei einer Irrtumswahrscheinlichkeit von 𝛼 = 0,01.
Lösung Beispiel 1:
Bestimmung der Häufigkeiten bei der unterstellten Gleichverteilung:
Es ist zuerst der Umsatz zu berechnen, der sich ergeben würde, wenn der Umsatz tatsächlich an allen Wochentagen gleich wäre (Verteilung der Hypothese). Dazu ist der Umsatz zu addieren und mit 1/𝑚, wobei 𝑚 die Anzahl der Realisationen (5 Tage) darstellt, zu multiplizieren:
Bestimmung der Prüfgröße: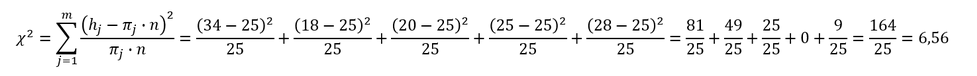
Bei Gleichverteilung würde jeder Tag einen Umsatz von 25 TEUR aufweisen. Für die Prüfgröße 𝜒^2 gilt:
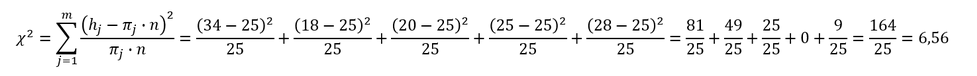
Bestimmung der oberen Grenze: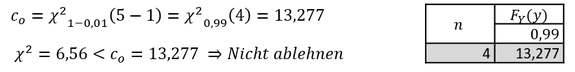
Zur Überprüfung der Hypothese der Gleichverteilung ist die obere Grenze in der 𝜒^2-Verteilung zu ermitteln. Dazu ist von der Anzahl der Realisationen 𝑚=5 die Zahl 1 zur Bestimmung des Freiheitsgrades abzuziehen. Für die obere Grenze gilt:
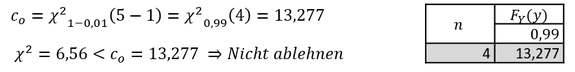
Die Nullhypothese ist nicht abzulehnen bzw. die Hypothese kann nicht verworfen werden.
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


