Gleichverteilung - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Spezielle Wahrscheinlichkeitsrechnung
Grundlagen der Gleichverteilung:
Die Gleichverteilung der Wahrscheinlichkeit von Zufallsvariablen ist eine der einfachsten Verteilungsformen. Dabei kommt jeder Realisation bzw. jedem unendlich kleinem Intervall die gleiche Eintrittswahrscheinlichkeit zuteil. Aufgrund dieser Besonderheit lassen sich die Funktionen der Verteilung, die Erwartungswerte und Varianzen sehr leicht bestimmen, wobei es zwischen diskreten und stetigen Zufallsvariablen zu unterscheiden gilt.
Wahrscheinlichkeitsfunktion gleichverteilter diskreter Zufallsvariablen:
Eine diskrete Zufallsvariable 𝑋 hat endlich abzählbar viele Realisationen 𝑥. Wird die Anzahl aller möglichen Realisationen der Zufallsvariablen mit 𝑛 bezeichnet, so kann die Wahrscheinlichkeit für den Eintritt einer Realisation sehr leicht mittels 1/𝑛 berechnet werden. Folglich gilt allgemein für die Wahrscheinlichkeitsfunktion einer gleichverteilten diskreten Zufallsvariablen:
Verteilungsfunktion gleichverteilter diskreter Zufallsvariablen: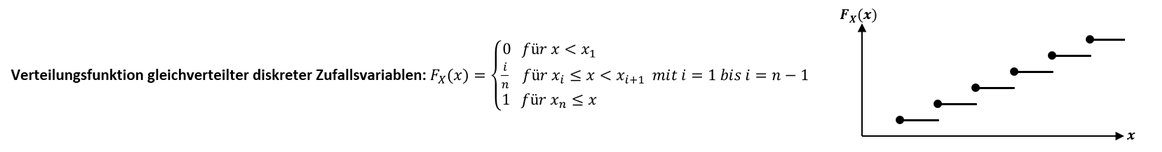
Werden die einzelnen Realisationen 𝑥 der Zufallsvariablen 𝑋 mit dem Index 𝑖 aufsteigend nach ihrer Reihenfolge gezählt 𝑥_(𝑖=1) ,𝑥_(𝑖=2) , …,𝑥_(𝑖=𝑛) , können die Wahrscheinlichkeiten der Verteilungsfunktion diskreter Zufallsvariablen allgemein über den Anzahlwert des Indexes in ihren Intervallen bestimmt werden, wobei die Wahrscheinlichkeit unterhalb der kleinsten Realisation 0 und oberhalb der höchsten Realisation 1 beträgt:
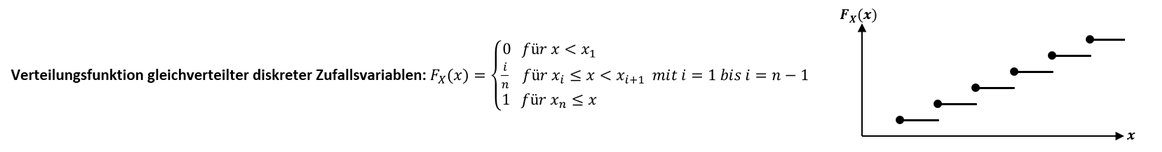
Erwartungswert und Varianz gleichverteilter diskreter Zufallsvariablen:
Stimmen die Werte der Realisationen 𝑥 der diskreten Zufallsvariablen 𝑋 mit der Zahl des Zählindexes 𝑖 überein, bzw. gilt mithin 𝑥_1=1, 𝑥_2=2, 𝑥_3=3…, also ist 𝑥_𝑖=𝑖, dann können die Parameter Erwartungswert und Varianz ganz leicht mit folgenden Formeln ermittelt werden:
Video "Gleichverteilung":
Das Probe-Video behandelt die Thematik "Gleichverteilung" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Wahrscheinlichkeitsfunktion gleichverteilter stetiger Zufallsvariablen:
Eine stetige Zufallsvariable 𝑋 ist im Falle der Gleichverteilung auf ein bestimmtes Intervall 𝑎,𝑏 begrenzt. Die Dichtefunktion kann mittels der Intervallgrenzen 𝑎,𝑏 sehr leicht ermittelt werden, indem man einen Bruch bildet, der im Zähler eine 1 stehen hat und im Nenner die Intervallgrenze 𝑎 von der Intervallgrenze 𝑏 subtrahiert wird. Wahrscheinlichkeiten außerhalb der Intervallgrenzen der Dichtefunktion betragen bekanntlich 0:
Verteilungsfunktion gleichverteilter stetiger Zufallsvariablen: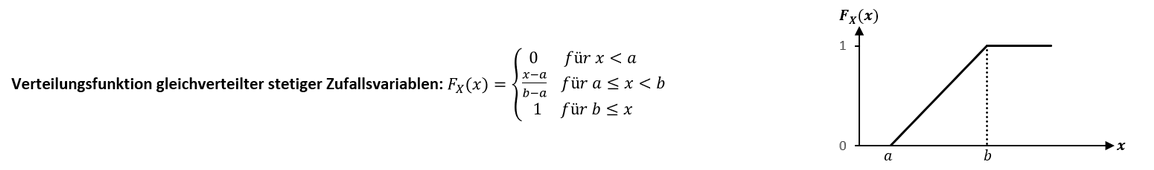
Auf eine Integration der Dichtefunktion zur Ermittlung der Verteilungsfunktion gleichverteilter stetiger Zufallsvariablen kann verzichtet werden. Allein mittels der Intervallgrenzen kann die Stammfunktion für die Dichtefunktion aufgeschrieben werden. Dazu ist wiederrum ein Bruch zu bilden, wobei diesmal im Zähler die Intervallgrenze 𝑎 von einer Realisation 𝑥 abzuziehen ist. Der Nenner bleibt dagegen identisch, wie bei der Wahrscheinlichkeitsfunktion:
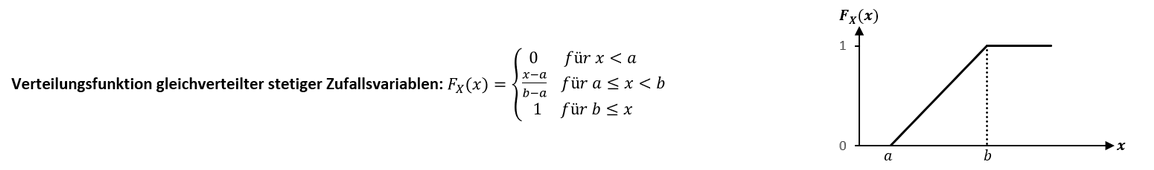
Erwartungswert und Varianz gleichverteilter stetiger Zufallsvariablen:
Die Parameter Erwartungswert und Varianz können bei einer gleichverteilten stetigen Zufallsvariable sehr leicht mittels der folgenden Formeln ermittelt werden:
Grundlagen Statistik-Paket
24 h Lehrvideos
240 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.
