Intervallschätzung - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Statistische Schätzverfahren
Intervallschätzung:
Die Wahrscheinlichkeit, dass die Punktschätzung eines unbekannten Parameters den tatsächlichen Wert des unbekannten Parameter 𝜃 liefert, ist äußerst gering. Die Aussagekraft einer Punktschätzung über den wahren unbekannten Parameterwert hält sich daher stark in Grenzen. Allerdings kann eine Punktschätzung um eine Intervallschätzung ergänzt werden. Dabei wird ausgehend von der Punktschätzung ein Intervall um den Schätzwert gelegt. Ein solches Intervall bezeichnet man als Konfidenzintervall.
Merke: Die Punktschätzung dient als Ausgangspunkt für die Intervallschätzung
Definition Konfidenzintervall (Vertrauensintervall):
Als Konfidenzintervall bezeichnet man das Intervall, welches um die Punktschätzung gelegt wird und dessen Intervall den unbekannten Parameter 𝜃 überdecken soll. Da es sich bei der Punktschätzung um eine Zufallsvariable handelt, dessen Schätzwert abhängig von den Realisationen der Stichprobe ist, handelt es sich auch bei dem Konfidenzintervall und dessen Grenzen um ein Zufallsintervall. Das Konfidenzintervall hat den Vorteil, dass sich mittels diesem eine Wahrscheinlichkeitsaussage darüber treffen lässt, wie wahrscheinlich es ist, dass das Konfidenzintervall den unbekannten Parameter 𝜃 überdeckt. Die Gegenwahrscheinlichkeit des Konfidenzintervalls, also dass das Konfidenzintervall den wahren unbekannten Parameter 𝜃 eben nicht überdeckt, wird mit dagegen mit der Irrtumswahrscheinlichkeit 𝛼 bezeichnet. Für die Wahrscheinlichkeit, dass der unbekannte Parameter 𝜃 tatsächlich vom Konfidenzintervall überdeckt wird, wobei 𝑈 die untere und 𝑂 für obere Intervallgrenze darstellen soll, gilt folglich:
ACHTUNG: Die Wahrscheinlichkeit gilt dem Intervall, nicht dem unbekannten Parameter 𝜃. Eine Aussage, dass der unbekannte Parameter mit einer Wahrscheinlichkeit in das Intervall fällt, ist entsprechend nicht möglich! Aus diesem Grund wird oftmals die Wahrscheinlichkeit 1−𝛼 vor dem Konfidenzintervall notiert.
Vereinfachtes Beispiel:
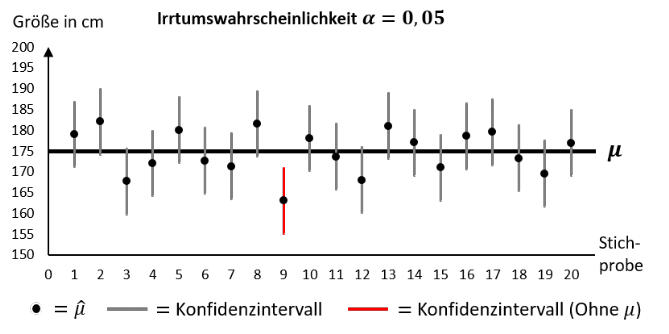
Wir wollen von unserem bekannten Beispiel der durchschnittlichen Größe aller in Deutschland lebenden Personen ausgehen. Dabei wollen wir zum Vergleich mit den Schätzungen aus der Stichprobe unterstellen, dass unser unbekannte Parameter der Grundgesamtheit den Erwartungswert 𝜇=175 annehmen würde. Daneben haben wir mittels 20 verschiedener Stichproben im Umfang von 𝑛=10000 unterschiedlichste Schätzwerte 𝜇 ̂ berechnet, um die ein 95%-Konfidenzintervall gelegt werden soll. Die Irrtumswahrscheinlichkeit beträgt folglich 𝛼 = 0,05 = 5%.
Video "Intervallschätzung":
Das Probe-Video behandelt die Thematik "Intervallschätzung" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Grundlagen Statistik-Paket
Übungen (optional)
24 h Lehrvideos
240 Skriptseiten
Formelsammlung
Klausurlösungen
Live-WebinareDas Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.
