Konfidenzintervall - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Statistische Schätzverfahren
Beispiele der Berechnung von Konfidenzintervallen für den Erwartungswert 𝝁:
Um die Vorgehensweise zur Berechnung des Konfidenzintervalls nochmals zu vertiefen, wollen wir ein paar Konfidenzintervalle berechnen.
Beispiel 1:
Aus einer endlichen Grundgesamtheit mit 𝑁 = 10.000 wurde eine Stichprobe im Umfang von 𝑛 = 50 erhoben. Die Stichprobe ergab einen Schätzwert für den Parameter 𝜇 ̂ = 225. Die Standardabweichung der Grundgesamtheit beträgt 𝜎 = 9. Wie lautet das zweiseitige Konfidenzintervall bei einer Irrtumswahrscheinlichkeit von 1%?
Lösung 1:
Es handelt sich um ein zweiseitiges Konfidenzintervall und die Standardabweichung ist bekannt. Für den Stichprobenumfang ergibt sich 𝑛/𝑁 = 50/10000 = 0,005 < 0,05, sodass keine Endlichkeitskorrektur vorgenommen werden muss. Es gilt bei 𝛼 = 0,01:
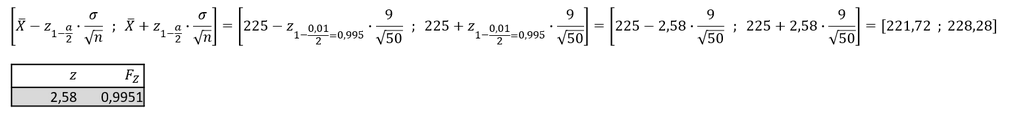
Das Konfidenzintervall [221,72 ; 228,28] überdeckt mit einer Wahrscheinlichkeit von 99% den tatsächlichen Erwartungswert 𝜇.
Beispiel 2:
Aus einer endlichen Grundgesamtheit mit 𝑁 = 500 wurde eine Stichprobe im Umfang von 𝑛 = 30 erhoben. Die Stichprobe ergab einen Schätzwert für den Parameter 𝜇 ̂ = 504. Die Varianz beträgt 𝑆^2 = 64. Wie lautet das zweiseitige Konfidenzintervall bei einer Irrtumswahrscheinlichkeit von 0,1%?
Lösung 2:
Es handelt sich um ein zweiseitiges Konfidenzintervall, wobei die Standardabweichung unbekannt ist (𝑆) und für 𝑛 gilt 𝑛 ≤ 30. Für den Stichprobenumfang ergibt sich 𝑛/𝑁 = 30/500 = 0,06 > 0,05, sodass eine Endlichkeitskorrektur vorgenommen werden muss. Es gilt bei 𝛼 = 0,001:
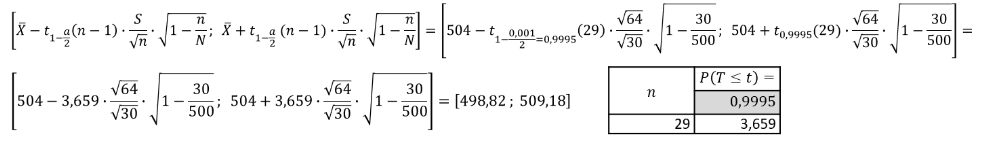
ACHTUNG: Die Klammer (𝑛−1) bezeichnet die Anzahl der Freiheitsgrade der 𝑡-Verteilung.
Video "Konfidenzintervall":
Das Probe-Video behandelt die Thematik "Konfidenzintervall" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Grundlagen Statistik-Paket
24 h Lehrvideos
240 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.
