Kontingenzkoeffizient - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Zweidimensionale Häufigkeitsverteilung
Kontingenzkoeffizient:
Der Kontingenzkoeffizient stellt eine Maßzahl für die Ausgeprägtheit/Stärke eines Zusammenhangs zwischen zwei nominalskalierten Merkmalen dar. Die Angabe der Stärke/Ausgeprägtheit eines Zusammenhangs trifft keine Aussage darüber, welche Art von Zusammenhang tatsächlich besteht, sondern nur, ob ein Zusammenhang vorliegt oder nicht. Ein starker Zusammenhang besteht also beispielsweise sowohl bei einem linearen Zusammenhang als auch bei einem nichtlinearen quadratischen Zusammenhang. Damit liefert der Kontingenzkoeffizient die geringsten Informationen der verschiedenen Koeffizienten.
Merke: Da der Kontingenzkoeffizient keine Informationen über die Art des Zusammenhangs liefert, besitzt dieser die Eigenschaft der Invarianz. Das bedeutet, dass ein Vertausch von Spalten oder Zeilen innerhalb der Kontingenztabelle zu keinerlei Veränderung des Kontingenzkoeffizienten führt.
Berechnung des Kontingenzkoeffizienten:
Der Kontingenzkoeffizient wird mit dem Symbol 𝐶 beschrieben, wobei zur Berechnung des Kontingenzkoeffizienten die Hilfsgröße Chi-Quadrat Χ^2 benötigt wird. Zur Berechnung von Chi-Quadrat Χ^2 sind die jeweiligen Randverteilungen miteinander zu multiplizieren und anschließend durch die Gesamtanzahl aller Merkmalskombinationen 𝑛 zu dividieren. Dieses Ergebnis ist dann von der jeweiligen absoluten Häufigkeit der Merkmalskombination abzuziehen und anschließend zu quadrieren. Das Ergebnis der quadrierten Subtraktion ist schließlich erneut durch das Ergebnis der Randverteilung der Multiplikation und anschließender Division durch 𝑛 zu dividieren. Die Summe aller Merkmalskombinationen, die dieser Berechnung unterzogen wurden, stellt dann das Chi-Quadrat Χ^2 dar:
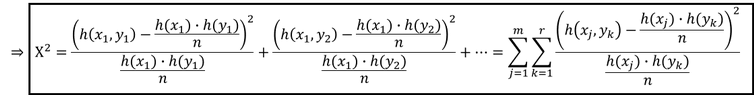
Mit der Hilfsgröße Chi-Quadrat Χ^2 lässt sich der Kontingenzkoeffizient 𝐶 berechnen. Dazu ist die Wurzel aus dem Ergebnis von Chi-Quadrat Χ^2 durch die Gesamtanzahl aller Merkmalskombinationen 𝑛 addiert mit Chi-Quadrat Χ^2 zu ziehen:
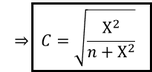
Merke: Zur Berechnung des Kontingenzkoeffizienten und seiner Hilfsgröße Chi-Quadrat sollte immer eine Erweiterung der Kontingenztabelle durchgeführt werden. Diese ermöglicht eine leichtere Berechnung der Hilfsgröße Chi-Quadrat und damit auch des Kontingenzkoeffizienten.
Interpretation der Maßzahl des Kontingenzkoeffizienten:
Beim Kontingenzkoeffizienten handelt es sich nicht um eine standardisierte Maßzahl, die Werte im Bereich von −1 und 1 [−1;1] annehmen kann. Erst durch die Berechnung des korrigierten Kontingenzkoeffizienten 𝐶_𝑘𝑜𝑟𝑟 wird die Maßzahl standardisiert und nimmt allerdings nur Werte im Bereich von 0 und 1 [0≤𝐶_𝑘𝑜𝑟𝑟≤1] an:
𝐶_𝑘𝑜𝑟𝑟 = 0: Kein Zusammenhang der Merkmale
𝐶_𝑘𝑜𝑟𝑟 = 1: Eindeutiger Zusammenhang der Merkmale
Video "Kontingenzkoeffizient":
Das Probe-Video behandelt die Thematik "Kontingenzkoeffizient" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Erweiterung der Kontingenztabelle:
Die Erweiterung der Kontingenztabelle ermöglicht eine vereinfachte und übersichtliche Berechnung der Hilfsgröße Chi-Quadrat. Dazu erfolgen die Teilberechnung der Merkmalskombinationen für die Ermittlung der Hilfsgröße bereits innerhalb der Felder, in dem die absoluten Häufigkeiten der Merkmalskombinationen angegeben sind. Diagonal nach unten rechts von der angegebenen Häufigkeit der Merkmalskombination ist dazu die Multiplikation der passenden Randverteilungen und anschließende Division durch 𝑛 zu notieren. Links von dieser Berechnung ist dann die Differenz zwischen der angegebenen Häufigkeitsverteilung und der Multiplikation zu berechnen. Davon ausgehend ist diagonal nach oben rechts die Differenz zu quadrieren. Die jeweiligen Teilergebnisse lassen sich durch Bildung eines Bruchs aus der rechten oberen und unteren Zahl herausfinden und sind nur noch zu addieren um zu Chi-Quadrat zu gelangen. Die Berechnung des allgemeinen Feldes lautet dann wie folgt:

Beispiel:

Wir wollen die Erweiterung des Feldes der ersten Merkmalskombination anhand folgender unterstellter Kontingenztabelle vornehmen:

Erweiterung der ersten Merkmalskombination:

Die Teilberechnung der ersten Merkmalskombination für Chi-Quadrat lautet: 0,64/8,8 .
Beispielhafte Bestimmungen des Kontingenzkoeffizienten:
Zur Veranschaulichung der Berechnung des Kontingenzkoeffizienten soll die Maßzahl anhand zweier Merkmale 𝑋 und 𝑌 erfolgen. Dabei soll das Merkmal 𝑋 die gewünschten Koalitionen und das Merkmal 𝑌 dagegen die Wahlentscheidung angeben. Insgesamt ergab die Erhebung folgende Merkmalskombinationen:
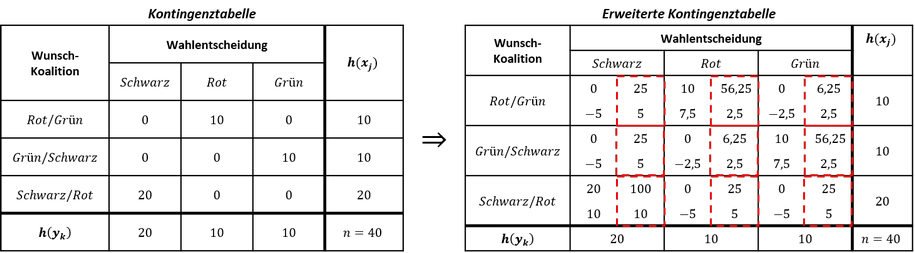
Zur Ermittlung des Kontingenzkoeffizienten ist die angegebene Kontingenztabelle zu erweitern, um leichter die Hilfsgröße Chi-Quadrat errechnen zu können. Die zu summierenden Werte für die Hilfsgröße Chi-Quadrat Χ^2 lassen sich in der erweiterten Kontingenztabelle durch die Bildung des Quotienten der rechten Werte neben der Häufigkeitsverteilung der Merkmalsausprägungen bilden:
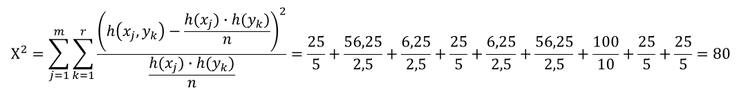
Mit der Hilfsgröße Chi-Quadrat Χ^2 lässt sich der Kontingenzkoeffizient 𝐶 ermitteln:
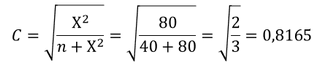
ACHTUNG: Eine Aussage über die Stärke des Zusammenhangs im Bereich von 0 bis 1 [0,1] kann erst anhand des korrigierten Kontingenzkoeffizienten erfolgen, da nur dieser standardisiert ist!
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


