Mittlere quadratische Abweichung - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Statistische Schätzverfahren
Mathematische mittlere quadratische Abweichung:
Die mittlere quadratische Abweichung, welche mit den Buchstaben 𝑀𝑆𝐸 (für: mean square error) notiert wird, bezeichnet die quadrierte Streuung von Werten um einen bestimmten Parameter. Bezüglich einer Schätzfunktion 𝑇 ist die mathematische mittlere quadratische Abweichung von zwei Faktoren abhängig, zum einen von der Varianz und zum anderen von einer sogenannten Bias (Verzerrung). Mathematisch kann die mittlere quadratische Abweichung für eine Schätzfunktion 𝑀𝑆𝐸 (𝑇) wie folgt notiert werden:
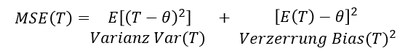
Varianz 𝑽𝒂𝒓(𝑻) der Schätzfunktion:
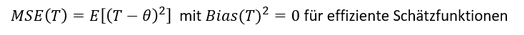
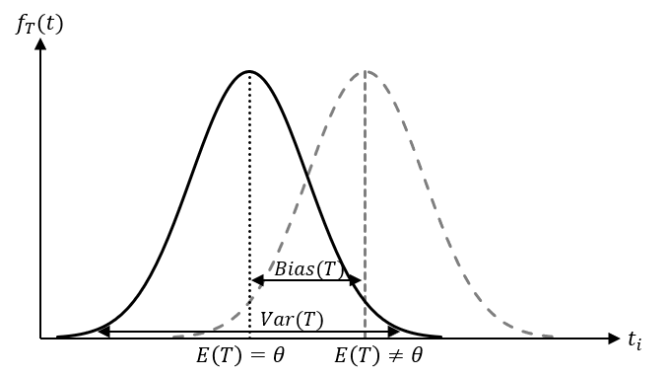
Der Erwartungswert der quadrierten Abweichungen von Schätzwerten 𝑇 (Mittelwert der quadratischen Abweichungen) vom tatsächlichen unbekannten Parameter 𝜃 entspricht der Berechnung der Varianz. Die Verwendung des Parameters Erwartungswert kann hier etwas in die Irre führen. Der Erwartungswert bezeichnet den Mittelwert, welchen wir sonst bei der Varianz mit 1/𝑛 ausgerechnet haben.
Verzerrung 𝑩𝒊𝒂𝒔(𝑻) der Schätzfunktion:
Als Verzerrung bezeichnet man die Abweichung des Erwartungswertes der Schätzwerte 𝑇 von dem tatsächlich unbekannten Parameter 𝜃. Eine Verzerrung kann nur im Falle nicht erwartungstreuer Schätzfunktionen eintreten, also wenn sich trotz genügender Punktschätzungen deren Erwartungswert nicht dem tatsächlichen unbekannten Parameter entspricht.
Mittlere quadratische Abweichungen von effizienten Schätzfunktionen:
Da effiziente Schätzfunktionen immer erwartungstreu sind, ergibt sich die Verzerrung (𝐵𝑖𝑎𝑠(𝑇)) zu 0, denn für eine erwartungstreue Schätzfunktion gilt 𝐸(𝑇) = 𝜃. Das bedeutet, dass die mittlere quadratische Abweichung einer effizienten Schätzfunktion lediglich von der Varianz 𝑉𝑎𝑟(𝑇) abhängig ist, die es bekanntlich zu minimieren gilt:
Merke: Effiziente Schätzfunktionen weisen keine Verzerrung/Bias auf!
Video "Mittlere quadratische Abweichung":
Das Probe-Video behandelt die Thematik "Mittlere quadratische Abweichung" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Grundlagen Statistik-Paket
24 h Lehrvideos
240 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.
