Summenhäufigkeit - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Eindimensionale Häufigkeitsverteilung
Grundlage der Summenhäufigkeitsverteilung:
Benötigt man Informationen über die Anzahl aller Merkmalsausprägungen, welche unterhalb oder oberhalb einer bestimmten Merkmalsausprägung liegen, ist auf die Summenhäufigkeitsverteilung zurückzugreifen. Die Summenhäufigkeitsverteilung gibt die Summe der jeweiligen nach ihrer Reihenfolge aufaddierten Merkmalsausprägungen an. Mittels der absoluten und relativen Summenhäufigkeit lässt sich entweder die Gesamtanzahl oder die prozentuale Anzahl bis zu einem bestimmten Merkmal ablesen.
Absolute Summenhäufigkeit:
Die absolute Summenhäufigkeit gibt die Gesamtanzahl der gezählten Merkmalsausprägungen bis zu einer bestimmten Merkmalsausprägung an. Dazu sind die Anzahlen der jeweiligen Merkmalsausprägungen nach ihrer Reihenfolge zu kumulieren (aufzuaddieren). Die absolute Summenhäufigkeit wird mit der Variable 𝐻_𝑗 beschrieben, wobei die Variable für die Gesamtanzahl bis zu einer bestimmten Merkmalsausprägung 𝐻(𝑥_𝑗) lautet.
Beispiel:
Relative Summenhäufigkeit:
Die relative Summenhäufigkeit gibt die kumulierte prozentuale Zahl der Merkmalsausprägungen bis zu einer bestimmten Merkmalsausprägung an. Dazu sind die Prozentsätze der jeweiligen Merkmalsausprägungen nach ihrer Reihenfolge zu kumulieren (aufzuaddieren). Die relative Summenhäufigkeit wird mit der Variable 𝐹_𝑗 beschrieben, wobei die Variable für die kumulierte relative Anzahl bis zu einer bestimmten Merkmalsausprägung 𝐹(𝑥_𝑗) lautet.
Beispiel:
Video "Summenhäufigkeit":
Das Probe-Video behandelt die Thematik "Summenhäufigkeit" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Beispiel einer Summenhäufigkeitsverteilung eines diskreten Merkmals:
Zum besseren Verständnis der absoluten und relativen Summenhäufigkeitsverteilung, wollen wir unser Beispiel mit dem Datenmaterial des Merkmals „Note“ einer Klausur fortführen. Dabei sind uns bereits die absoluten und relativen Häufigkeiten der Merkmalsausprägungen bekannt:
Absolute und relative Summenhäufigkeiten:
Zur Ermittlung der absoluten und relativen Summenhäufigkeiten der bereits vorliegenden Häufigkeiten, sind diese lediglich nach ihrer Reihenfolge von „sehr gut“ bis „nicht ausreichend“ aufzuaddieren:
Grafische Darstellung der Häufigkeits- und Summenhäufigkeitsverteilung:
Lassen sich die Häufigkeitsverteilungen diskreter Merkmalsausprägungen in einem Stab-, Balken- oder Säulendiagramm darstellen, bedarf es zur Darstellung von Summenhäufigkeitsverteilungen diskreter Merkmalsausprägungen einer Treppenfunktion:
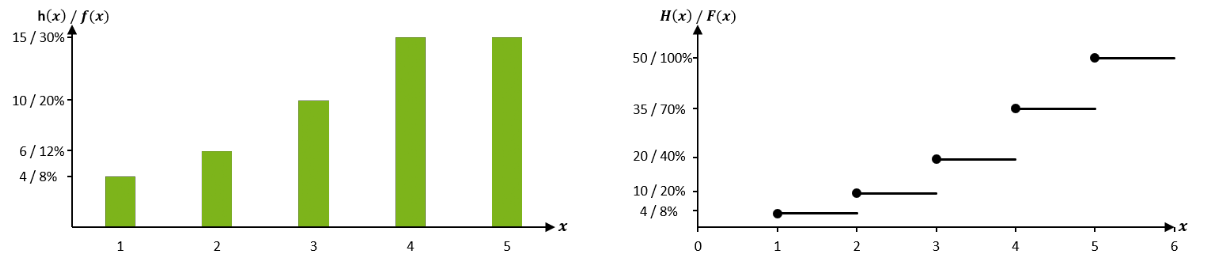
Grundlagen Statistik-Paket
240 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)
24 h LehrvideosDas Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.
