Unabhängigkeit von Merkmalen - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Zweidimensionale Häufigkeitsverteilung
Grundlage der (Un-)Abhängigkeit von Merkmalen:
Zwischen zwei Merkmalen 𝑋 und 𝑌 kann eine Abhängigkeit oder Unabhängigkeit bestehen. Dabei besagt die Abhängigkeit zweier Merkmale 𝑋 und 𝑌, dass ein gewisser Zusammenhang zwischen den beiden Merkmalen besteht. Das bedeutet, dass mittels des Wissens einer Merkmalsausprägung in gewissem Maße auf die Merkmalsausprägung des anderen Merkmals geschlossen werden kann. Die Unabhängigkeit hingegen besagt, dass keinerlei Zusammenhang zwischen den beiden Merkmalen besteht, entsprechend existiert keinerlei Zusammenhang zwischen den Merkmalsausprägungen.
Beispiel der Abhängigkeit zweier Merkmale:
Die beiden Merkmale Körpergröße und Gewicht sind beispielsweise in gewissem Maße abhängig voneinander. So ist davon auszugehen, dass mit steigender Körpergröße auch das Gewicht in gewissem Maße steigt.
Beispiel der Unabhängigkeit zweier Merkmale:
Die beiden Merkmale Geschlecht und Nationalität sind beispielsweise unabhängig voneinander. Mittels des Wissens über das Geschlechts eines Menschen lässt sich keine Aussage über dessen Herkunft treffen.
Mathematische Ermittlung der Unabhängigkeit von Merkmalen:
Die Unabhängigkeit zweier Merkmale lässt sich mittels der bedingten Verteilung prüfen. Denn Unabhängigkeit von Merkmalen liegt genau dann vor, wenn die Verteilung eines Merkmals nicht vom anderen Merkmal beeinflusst wird. Stimmen die bedingten Verteilungen des Merkmals mit der Randverteilung des Merkmals überein, so nimmt das andere Merkmal keinerlei Einfluss auf dessen Verteilung. Für die Unabhängigkeit von Merkmalen muss entsprechend gelten:
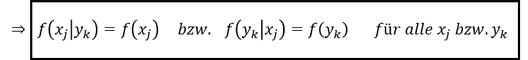
Für die Unabhängigkeit zweier Merkmale muss allgemein folgendes gelten:

Merke: Stimmt auch nur eine bedingte Verteilung eines Merkmals nicht mit der Randverteilung des Merkmals überein, sind die Merkmale abhängig!
Mathematische Umformung zur Vereinfachung der Ermittlung der Unabhängigkeit von Merkmalen:
Zur Prüfung auf die Unabhängigkeit von Merkmalen haben wir bisher die bedingten Verteilungen mit den Randverteilungen verglichen. Die Gleichung zur Ermittlung der Unabhängigkeit von Merkmalen lässt sich jedoch umformen, sodass wir mittels der Randverteilungen auf die Häufigkeitsverteilung der Merkmalskombinationen schließen können. Diese Vorgehensweise erspart uns gerade bei angegebenen absoluten Häufigkeiten viel Zeit.
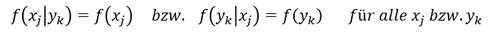
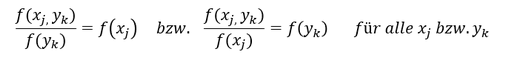
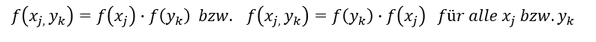
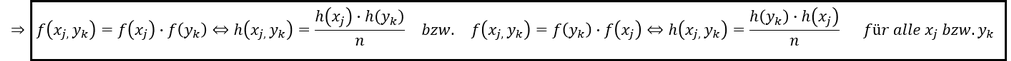
Mathematische Umformung der Gleichung für die Unabhängigkeit von Merkmalen:
Für die Ermittlung der Unabhängigkeit von Merkmalen galt folgender mathematischer Zusammenhang:
Aus den bedingten Verteilungen wissen wir, dass 𝑓(𝑥_𝑗│𝑦_𝑘 )=(𝑓(𝑥_(𝑗, ) 𝑦_𝑘))/(𝑓(𝑦_𝑘)) bzw. das 𝑓(𝑦_𝑘│𝑥_𝑗 )=(𝑓(𝑥_(𝑗, ) 𝑦_𝑘))/(𝑓(𝑥_𝑗)) entspricht. Ersetzen wir die bedingten Verteilungen mit ihrer mathematischen Gleichung, gelangen wir für die Unabhängigkeit von Merkmalen zu folgendem Zusammenhang:
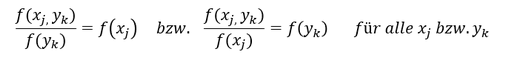
Diese Gleichungen lassen sich nun durch die Multiplikation mit dem Nenner umformen, sodass sich Gleichungen aufgelöst nach der relativen Häufigkeitsverteilung der Merkmalskombinationen ergeben:
Da wir wissen, dass die relative Häufigkeit nichts anderes darstellt als die absolute Häufigkeit geteilt durch die Gesamtanzahl aller Merkmalskombinationen 𝑛, können wir schließlich auch die absoluten Häufigkeiten für die Merkmalskombinationen bei Unabhängigkeit der Merkmale mittels der Randverteilungen ermitteln:
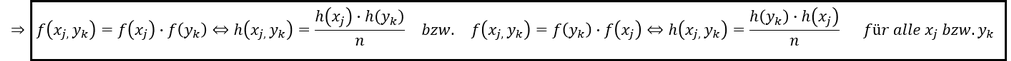
Vereinfachung der Prüfung auf die Unabhängigkeit von Merkmalen:
Aus der allgemeinen Gleichung zur Ermittlung der Unabhängigkeit von Merkmalen geht hervor, dass man neben dem Vergleich der bedingten Häufigkeiten mit der Randverteilung auch durch Multiplikation der jeweiligen Randverteilungen und ggf. Teilung durch 𝑛 prüfen kann, ob sich die richtige absolute/relative Häufigkeit für eine bestimmte Merkmalskombination ergibt. Stimmt die angegebene absolute/relative Häufigkeit der Merkmalskombination nicht mit dem Ergebnis der Multiplikation der jeweiligen Randverteilungen überein, sind die Merkmalsausprägungen abhängig voneinander.
Video "Unabhängigkeit von Merkmalen":
Das Probe-Video behandelt die Thematik "Unabhängigkeit von Merkmalen" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Beispiel mittels der Vereinfachung zur Prüfung von Unabhängigkeit bei Merkmalen:
Zur Veranschaulichung der Vereinfachung wollen wir nochmals von unserem vorhergehenden Beispiel ausgehen, mit der gemeinsamen Verteilung des Merkmals 𝑋 Geschlecht und des Merkmals 𝑌 Nationalität:

Die Prüfung, ob die Merkmale voneinander unabhängig sind, erfolgt nun nicht mehr über die bedingte Verteilung, sondern wir wollen prüfen, ob die angegebenen Häufigkeiten der Merkmalskombinationen sich aus der Multiplikation der Randverteilung und anschließender Division durch 𝑛 = 100 ergeben:
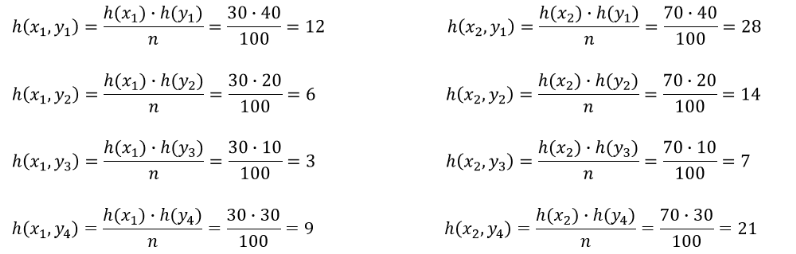
Die Häufigkeitsverteilung aller Merkmalskombinationen stimmt mit der Multiplikation der jeweiligen Randverteilung überein. Das bedeutet, dass die Merkmale unabhängig voneinander sind. Wäre nur eine Häufigkeit abgewichen, so wären die Merkmale abhängig voneinander gewesen.
Merke: Welche der beiden Methoden zur Prüfung auf Unabhängigkeit der Merkmale man wählt, bleibt einem selbst überlassen. Jedoch muss man beide Methoden nicht bis zum Ende durchführen, sobald auffällt, dass entweder eine bedingte Verteilung von der Randverteilung abweicht, oder eine angegebene Häufigkeit nicht mit der Multiplikation der Randverteilung übereinstimmt. Auch nur eine Abweichung führt bereits dazu, dass die Merkmale abhängig voneinander sind.
ACHTUNG: Die Prüfung auf Unabhängigkeit trifft keine Aussage darüber, inwieweit bei ermittelter Abhängigkeit die Merkmale voneinander abhängig sind, dafür dient die Korrelation.
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


