Verteilungsfunktion - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Wahrscheinlichkeitsrechnung
Grundlagen der Verteilungsfunktion diskreter Zufallsvariablen:
Als Verteilungsfunktion diskreter Zufallsvariablen bezeichnet man eine Funktion, die die aufaddierten zugeordneten Wahrscheinlichkeiten der Realisationen nach ihrer Reihenfolge wiedergibt. Die Verteilungsfunktion gibt damit die Wahrscheinlichkeit an, dass die diskrete Zufallsvariable in den Bereich vom Beginn der Wahrscheinlichkeitsfunktion bis zu einer bestimmten Realisation 𝑥 fällt und entspricht damit der bereits in der deskriptiven Statistik kennengelernten relativen Summenhäufigkeit. Es existiert gerade in Bezug auf die grafische Darstellung eine sehr enge Analogie zwischen Verteilungsfunktion und relativer Summenhäufigkeit diskreter Merkmalsausprägungen. Bezüglich der Notation unterscheidet sich allerdings die Verteilungsfunktion von der Summenhäufigkeit.
Merke: Der einzige Unterschied zwischen diskreter relativer Summenhäufigkeit und der Verteilungsfunktion diskreter Zufallsvariablen liegt in der Notation.
Notation der Verteilungsfunktion diskreter Zufallsvariablen:
Da, wie der Name schon sagt, es sich bei der Verteilungsfunktion um eine Funktion handelt, muss deren Notation auch als Funktion erfolgen, wobei Funktionen für alle reellen Zahlen definiert sind. Diese Eigenschaft führt dazu, dass die Notation der Verteilungsfunktion mittels der Bildung von Intervallen für die einzelnen Realisationen erfolgt. Die Verteilungsfunktion wird dabei, wie bei einer Summenhäufigkeit, mit dem Großbuchstaben 𝐹 notiert (𝐹_𝑋 (𝑥)). Eine Verteilungsfunktion hat im Allgemeinen folgendes Aussehen:
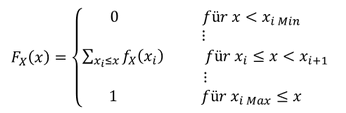
Eigenschaften der Verteilungsfunktion diskreter Zufallsvariablen:
Die Eigenschaften der Verteilungsfunktion beziehen sich zum einen auf die Definition der Verteilungsfunktion und zum anderen auf die grafischen Eigenschaften der Verteilungsfunktion.
Eigenschaften aus der Definition der Verteilungsfunktion:
𝐹_𝑋 (𝑥) = 𝑃(𝑋 ≤ 𝑥): Die Verteilungsfunktion entspricht der kumulierten Wahrscheinlichkeit aller Realisationen der Zufallsvariablen bis zur gewählten Realisation 𝑥.
𝐹_𝑋 (𝑥) = 𝑃(−∞ < 𝑋 ≤ 𝑥): Die Verteilungsfunktion entspricht der kumulierten Wahrscheinlichkeit zwischen minus unendlich bis zur gewählten Realisation. Da die Wahrscheinlichkeit unterhalb der kleinsten Realisation sowieso null beträgt, kann auch die Unendlichkeit als untere Grenze gewählt werden.
𝐹_𝑋 (𝑥) = ∑_(𝑥_𝑖≤𝑥) [(𝑓_𝑋 (𝑥_𝑖))]: Die Verteilungsfunktion entspricht der Summierung (Kumulierung) aller Wahrscheinlichkeiten der Zufallsvariablen bis zur gewählten Realisation 𝑥.
Grafische Eigenschaften der Verteilungsfunktion:
𝐹_𝑋 = 𝑚𝑜𝑛𝑜𝑡𝑜𝑛 𝑠𝑡𝑒𝑖𝑔𝑒𝑛𝑑: Wahrscheinlichkeiten können nur positiv oder gleich 0 sein. Eine Aufsummierung führt deshalb zu gleichen oder steigenden Wahrscheinlichkeit.
𝐹_𝑋 (𝑥) = 𝑃(𝑋 ≤ 𝑥): Die Verteilungsfunktion ist rechtsseitig stetig. Die Wahrscheinlichkeit bis zu einer Realisation wird „von rechts nach links“ abgelesen. (Mit Sprung)
𝐹_𝑋 (𝑥) = 𝑃(𝑋 < 𝑥): Die Verteilungsfunktion ist linksseitig stetig. Die Wahrscheinlichkeit bis zu einer Realisation wird „von links nach rechts“ abgelesen. (Ohne Sprung)
Mathematisches Beispiel der Verteilungsfunktion diskreter Zufallsvariablen:
Wir wollen unser Beispiel des Würfelwurfs bei der Wahrscheinlichkeitsverteilung diskreter Zufallsvariablen fortführen. Es ergaben sich folgende Wahrscheinlichkeiten der Realisationen:
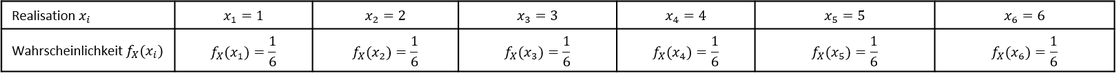
Mathematische Darstellung der Verteilungsfunktion diskreter Zufallsvariablen:
Die mathematische Darstellung der Verteilungsfunktion diskreter Zufallsvariablen erfolgt mittels des Funktionsintervalls. Dabei sind die Realisationen als Intervallgrenzen zu nutzen und die Wahrscheinlichkeit ist für die Intervalle aufzuaddieren. Das Funktionsintervall der Verteilungsfunktion dieses Beispiels würde lauten:

Die Eigenschaften aus der Definition der Verteilungsfunktion diskreter Zufallsvariablen werden eingehalten, wobei wir von der maximalen Realisation 𝑥=6 ausgehen wollen:
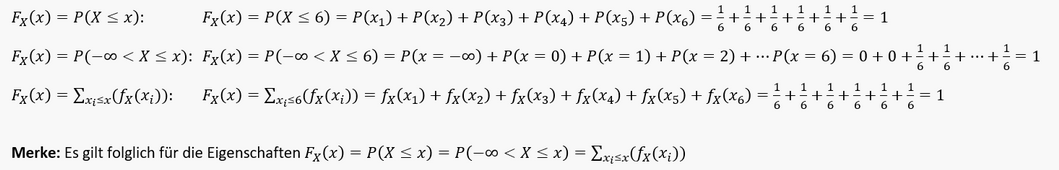
Video "Verteilungsfunktion":
Das Probe-Video behandelt die Thematik "Verteilungsfunktion" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Grafisches Beispiel der Verteilungsfunktion diskreter Zufallsvariablen:
Wir wollen unser Beispiel des Würfelwurfs aus dem mathematischen Beispiel der Verteilungsfunktion diskreter Zufallsvariablen fortführen.
Grafische Darstellung der Verteilungsfunktion diskreter Zufallsvariablen:
Die grafische Darstellung der Verteilungsfunktion diskreter Zufallsvariablen erfolgt mittels einer Treppenfunktion. Sobald ein neues Intervall erreicht wird, springt die Grafik eine „Stufe“ höher auf die neue kumulierte Wahrscheinlichkeit. Die kumulierten Wahrscheinlichkeiten der Realisationen lassen sich dabei auf der 𝑦-Achse ablesen. Die grafische Treppenfunktion für die Verteilungsfunktion hat folgendes Aussehen:

Die grafischen Eigenschaften der Verteilungsfunktion diskreter Zufallsvariablen werden eingehalten:

Merke: Die Ermittlung der Wahrscheinlichkeit eines Intervalls zwischen zwei Realisationen kann, wie bereits bei der Summenhäufigkeitsverteilung gelernt, durch Differenzbildung ermittelt werden. Dabei ist auf das kleiner < oder kleiner gleich ≤ Zeichen zu achten, ob die Wahrscheinlichkeit des Sprungs zur nächsten Realisation berücksichtigt wird oder nicht.
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


