Vorzeichentest - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Statistische Testverfahren
Vorzeichentest/Mediantest:
Der Vorzeichentest wird zur Prüfung einer Nullhypothese über den Median oder zum Vergleich zweier verbundener Stichproben verwendet. Dabei muss das Merkmal der Grundgesamtheit mindestens ordinalskaliert sein. Zur Prüfung der Nullhypothese steht das Vorzeichen bei der Bildung der Differenz zwischen den Stichprobenwerten und dem angenommenen Median bzw. der verbundenen Stichprobe im Vordergrund. Denn sollte der angenommene Median tatsächlich richtig sein, so müssten ungefähr die Hälfte der Stichprobenwerte oberhalb und die andere Hälfte unterhalb des angenommenen Medianwertes liegen. Gleiches gilt für den Vergleich zweier verbundener Stichproben, wenn angenommen wird, dass diese gleich sein sollen. Das Vorzeichen aus der Differenz dient also dem Erkennen, wie oft die Stichprobenwerte oberhalb/unterhalb des Medians bzw. einer verbundenen Stichprobe liegen. Zur Prüfung der Hypothese gilt es dann, die positiven Vorzeichen zu zählen, wobei sich nicht zu viele positive, aber auch nicht zu wenig positive Vorzeichen ergeben dürfen.
Merke: Bei verbundenen Stichproben handelt es sich um Stichproben, die zweimal in Folge unabhängig, aber unter den selben Bedingungen erhoben werden, sodass sich gepaarte Beobachtungen ergeben, die verglichen werden können.
ACHTUNG: Im Weiteren wollen wir ausschließlich auf den Vergleich zweier verbundener Stichproben eingehen.
Nullhypothesen des Vorzeichentests:
Die Nullhypothese des Vorzeichentests trifft eine Aussage über die Differenz zweier verbundener Stichproben. Dabei geht man bei der Nullhypothese meist davon aus, dass die Differenz im Mittel 0 beträgt, also dass sich die Stichproben nicht voneinander unterscheiden. Die Nullhypothese lautet im Allgemeinen:
Notwendige Angaben des Vorzeichentests:
Zur Durchführung des Vorzeichentests bedarf es lediglich über das Wissen der Wertepaare der verbundenen Stichproben. Meist ist der Differenzbetrag auch gleichzeitig angegeben, woran man in der Prüfung schnell erkennen kann, dass es sich um den Vorzeichentest handelt. Die Angabe der Wertepaare erfolgt dabei meist in Tabellenform, wobei die Wertepaare (meist 𝑋,𝑌) untereinander notiert werden, da es sich hierbei um unabhängige, aber gleiche Erhebungsbedingungen handelt.

Allgemeine Durchführung des Vorzeichentests/Mediantests:
Zur allgemeinen Prüfung, ob die Nullhypothese über die Differenz zweier verbundener Stichproben abzulehnen ist, bedarf es einer Prüfgröße und kritischer Werte bzw. Grenzen, die den Ablehnungsbereich definieren. Als Prüfgröße des Vorzeichentests dient die Anzahl positiver Vorzeichen, was dem 𝑥-Wert in der Binomialverteilung entspricht, da es bei der Prüfung des Vorzeichens nur zwei mögliche Realisationen geben kann (positiv/negativ). Die Grenzen für den Ablehnungsbereich lassen sich dann mittels der angegebenen Irrtumswahrscheinlichkeit 𝛼 in der Binomialverteilung finden.
Mathematische Ermittlung der Prüfgröße des Vorzeichentests/Mediantests:
Die Ermittlung der Prüfgröße erfolgt durch die Differenzbildung 𝐷_𝑖 der verbundenen Stichprobenwerte 𝑥_𝑖 und 𝑦_𝑖. Ergibt sich eine Differenz größer 0, so ist dieser Differenz 𝐷_𝑖 die Zahl 𝑍_𝑖 = 1 zuzuordnen, ist die Differenz kleiner 0, so ist die Zahl 𝑍_𝑖 = 0 zuzuordnen. Die Summierung aller zugeordneten Zahlen 𝑍_𝑖 entspricht der Anzahl positiver Differenzen. Dieser Wert gilt als Prüfgröße für die Binomialverteilung, wie oft das Ereignis „Positive Differenz“ eingetreten ist:
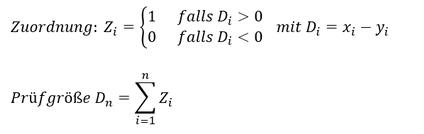
Merke: Auf die Zuordnungen kann verzichtet werden. Die Prüfgröße entspricht einfach der Anzahl positiver Differenzen.
Ermittlung der kritischen Werte/Grenzen des Vorzeichentests/Mediantests:
Der Vorzeichentest kann sowohl eine obere als auch untere Grenze (zweiseitig) oder nur eine obere/untere Grenze (einseitig) aufweisen. Sobald die Grenzen unter bzw. überschritten werden, ist der Unterschied zwischen den Stichproben so einseitig, dass die Nullhypothese, dass beide Stichproben gleich sind, abzulehnen ist. Die Ermittlung der Grenzen erfolgt dabei wie beim Test für den Anteilswert. Es ist der x-Wert als untere/obere Grenze in der Binomialverteilung zu wählen, sobald in der Verteilungsfunktion die Wahrscheinlichkeit 𝛼/2 bzw. 1 − 𝛼/2 der Punkthypothese erstmals überschritten wird. Bei der Binomialverteilung ist der Parameter 𝜋 immer mit 𝜋 = 0,5 zu wählen und der 𝑛-Wert in Höhe des einzelnen Stichprobenumfangs abzüglich der Stichprobenpaare, die als Differenz 0 ergeben:

Video "Vorzeichentest":
Das Probe-Video behandelt die Thematik "Vorzeichentest" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Anwendungsbeispiel des Vorzeichentests/Mediantests:
Um die Vorgehensweise bei der Durchführung des Vorzeichentests besser verdeutlichen zu können, wollen wir ein Beispiel berechnen.
Beispiel 1:
Es soll geprüft werden, ob die Anzahl der konsumierten Fernsehstunden innerhalb der Woche gleich hoch sind wie am Wochenende. Dazu wurden gleiche Stichproben - einmal wochentags und einmal am Wochenende - ermittelt:

Es ist die Hypothese 𝐷_𝑀𝑒𝑑 = 0 zu prüfen, dass der Fernsehkonsum an Wochentagen und Wochenenden gleich hoch ist, bei einer Irrtumswahrscheinlichkeit von 𝛼 = 0,05.
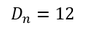
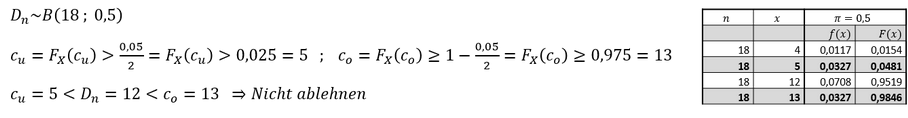
Lösung Beispiel 1:
Bestimmung der Prüfgröße:
Zur Bestimmung der Prüfgröße 𝐷_𝑛 sind die positiven Vorzeichen zu zählen:
Bestimmung der Grenzen:
Bei der Hypothese handelt es sich um eine Punkthypothese. Es ist eine untere und obere Grenze zu bestimmen. Bei der Binomialverteilung ist darauf zu achten, dass der Stichprobenumfang 𝑛 = 20 um den Wert 2 auf 𝑛 = 18 gesenkt wird, weil sich die Differenz zweier Wertepaare zu 0 (=) ergeben hat:
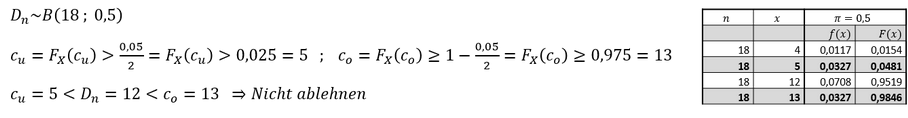
Die Nullhypothese ist nicht abzulehnen bzw. die Hypothese kann nicht verworfen werden.
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


