Wahrscheinlichkeitsfunktion - Grundlagen der Statistik - Fernuni Hagen
Grundlagen Statistik-Paket > Grundlagen-Statistik > Wahrscheinlichkeitsrechnung
Grundlagen der Wahrscheinlichkeitsverteilung diskreter Zufallsvariablen:
Als Wahrscheinlichkeitsverteilung diskreter Zufallsvariablen bezeichnet man die Darstellung aller möglichen Realisationen der Zufallsvariablen mit ihren jeweiligen Eintrittswahrscheinlichkeiten. Die Wahrscheinlichkeitsverteilung diskreter Zufallsvariablen weist damit enge Parallelen zur relativen Häufigkeitsverteilung in der deskriptiven Statistik auf. Die Darstellung der Wahrscheinlichkeitsverteilung erfolgt ebenfalls, wie bei der relativen Häufigkeitsverteilung, in tabellarischer Form. Dabei wird den Realisationen 𝑥_𝑖 der Zufallsvariable 𝑋 die Wahrscheinlichkeiten für deren Eintreten 𝑓_𝑋 (𝑥_𝑖) zugeordnet. Die allgemeine tabellarische Wahrscheinlichkeitsverteilung einer diskreten Zufallsvariable hat folgendes Aussehen:
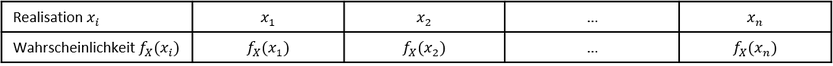
Achtung: Trotz enger Analogie zwischen relativer Häufigkeitsverteilung und Wahrscheinlichkeitsverteilung stellen die Verteilungen vollkommen unterschiedliche Sachverhalte dar. Während die relative Häufigkeitsverteilung die relative (prozentuale) Häufigkeit der jeweiligen beobachteten Merkmalsausprägungen wiedergibt, gibt die Wahrscheinlichkeitsverteilung lediglich die Wahrscheinlichkeiten für das Eintreten einer Realisation bei einem Zufallsexperiment an. Die Angabe der Wahrscheinlichkeiten stellen keine tatsächlich eingetretenen Ergebnisse dar!
Wahrscheinlichkeitsfunktion diskreter Zufallsvariablen:
Die Zuordnungsvorschrift der Wahrscheinlichkeiten zu den Realisationen wird als Wahrscheinlichkeitsfunktion bezeichnet. Eine Funktion beschreibt im Allgemeinen eine Beziehung zwischen zwei Mengen, wobei jedem Element der einen Menge genau ein Element der anderen Menge zuordnet ist. Dieser Sachverhalt ist bei der Zuordnung der Wahrscheinlichkeiten zu den Realisationen gegeben. Die „Menge“ der Wahrscheinlichkeit ist abhängig von der „Menge“ der Realisation. Die allgemeine Darstellung der Wahrscheinlichkeitsfunktion erfolgt durch eine funktionale Darstellung der Tabelle der Wahrscheinlichkeitsverteilung:
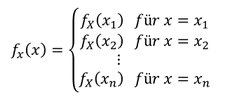
Eigenschaften der Wahrscheinlichkeitsfunktion:
Die Eigenschaften der Wahrscheinlichkeitsfunktion entspringen aus der Definition der Wahrscheinlichkeit. Es gelten folgende wichtige Eigenschaften für die Wahrscheinlichkeitsfunktion:

Merke: Die tabellarische als auch grafische Darstellung der Wahrscheinlichkeitsfunktion bei diskreten Zufallsvariablen entspricht der bereits gelernten relativen Häufigkeitsverteilung. Den einzigen Unterschied, den man sich eigentlich merken muss ist, dass die Wahrscheinlichkeitsverteilung eben die Wahrscheinlichkeiten und nicht die Häufigkeit angibt.
Video "Wahrscheinlichkeitsfunktion":
Das Probe-Video behandelt die Thematik "Wahrscheinlichkeitsfunktion" des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Grundlagen Statistik-Pakets.
Alle Thematiken des vollständigen Videos
Beispiel der Wahrscheinlichkeitsfunktion diskreter Zufallsvariablen:
Wir wollen uns sowohl die mathematische Darstellung als auch die grafische Darstellung der Wahrscheinlichkeitsfunktion nochmal anhand eines Beispiels veranschaulichen. Dazu wollen wir von dem bereits beschriebenen Beispiel des Würfelwurfs ausgehen, wobei die Realisationen 𝑥_𝑖 Werte von 1-6 angenommen haben und die Wahrscheinlichkeit bei 1/6 für jede Realisation lag.
Mathematische Darstellung der Wahrscheinlichkeitsfunktion diskreter Zufallsvariablen:
Die mathematische Darstellung der Wahrscheinlichkeitsverteilung diskreter Zufallsvariablen erfolgt mittels der Tabellenform oder der Funktion. Es sind einfach nur die Realisationen und deren zugeordnete Wahrscheinlichkeiten in einer Tabelle oder Funktion aufzulisten:

Die Eigenschaften der Wahrscheinlichkeitsfunktion diskreter Zufallsvariablen werden eingehalten:
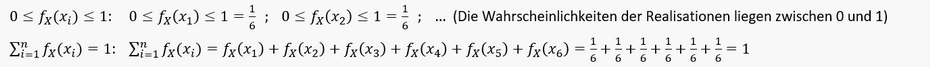
Grafische Darstellung der Wahrscheinlichkeitsfunktion diskreter Zufallsvariablen:
Die grafische Darstellung der Wahrscheinlichkeitsfunktion diskreter Zufallsvariablen erfolgt mittels eines Stab- oder Säulendiagramms. Dabei kann die Wahrscheinlichkeit für jede Realisation auf der 𝑦-Achse abgelesen werden:
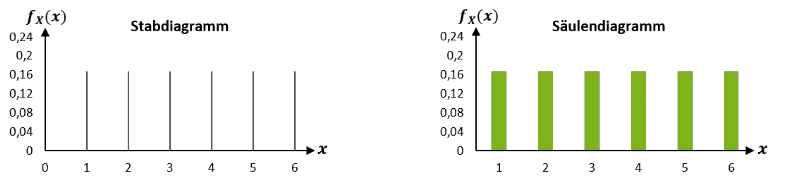
Grundlagen Statistik-Paket
Das Grundlagen Statistik-Paket enthält den gesamten statistischen Teil des Kurses "Grundlagen der Statistik" des Moduls "Grundlagen der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket erfordert keinerlei großen statistischen Vorkenntnisse und ist ausgerichtet auf das erfolgreiche Bestehen der Klausur. Der Aufbau folgt den Kursskripten der Fernuni Hagen und behandelt dabei alle wichtigen Themen. Optional zum Paket stehen noch über 160 Übungsaufgaben und Übungsklausuren zur Verfügung.


