Definitheit Hesse-Matrix - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Extrema nicht-linearer Funktionen
Extrema und Sattelpunkte von mehrdimensionalen Funktionen:
Die kritischen Punkte von Funktionen mehrerer Variabler können lokale/globale Extremstellen (Minima/Maxima) oder Sattelpunkte der Funktion sein. Um zu überprüfen, ob es sich bei einem kritischen Punkt um ein Extremum oder Sattelpunkt handelt, sind alle zweiten partiellen Ableitungen der Funktion zu bestimmen und als Hesse-Matrix anzugeben. Werden dann die Werte des kritischen Punktes in die zweiten partiellen Ableitungen der Hesse-Matrix eingesetzt und die Funktionswerte ermittelt, so lässt sich mittels der Definitheit der Hesse-Matrix bestimmen, ob es sich bei dem kritischen Punkt um ein Minimum, ein Maximum oder ein Sattelpunkt handelt. Denn im Falle eines Minimums bzw. Maximums ergibt sich eine positive bzw. negative Definitheit der Hesse-Matrix. Im Falle eines Sattelpunktes ist die Hesse-Matrix dagegen indefinit. Allgemein kann also ein Extremum oder Sattelpunkt wie folgt über die Definitheit der Hesse-Matrix mit eingesetzten kritischen Punkt 𝐇 𝑓(𝒙^((0) )) bestimmt werden:
𝐇 𝑓(𝒙^((0) ) ) = 𝑝𝑜𝑠𝑖𝑡𝑖𝑣 𝑑𝑒𝑓𝑖𝑛𝑖𝑡 ⇒ 𝑀𝑖𝑛𝑖𝑚𝑢𝑚
𝐇 𝑓(𝒙^((0) ) ) = 𝑛𝑒𝑔𝑎𝑡𝑖𝑣 𝑑𝑒𝑓𝑖𝑛𝑖𝑡 ⇒ 𝑀𝑎𝑥𝑖𝑚𝑢𝑚
𝐇 𝑓(𝒙^((0) ) ) = 𝑖𝑛𝑑𝑒𝑓𝑖𝑛𝑖𝑡 ⇒ 𝑆𝑎𝑡𝑡𝑒𝑙𝑝𝑢𝑛𝑘𝑡
Beispielhafte Bestimmung von Extrema und Sattelpunkte einer mehrdimensionalen Funktion:
Zum besseren Verständnis der Bestimmung von Extrema oder Sattelpunkten wollen wir die folgende mehrdimensionale Funktion unterstellen, wobei die Funktion folgende kritische Punkte aufweist:
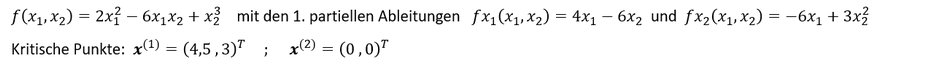
Bestimmung der allgemeinen Hesse-Matrix mit den 2. partiellen Ableitungen:
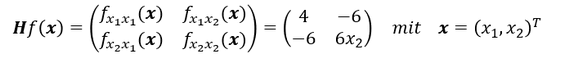
Bestimmung der Hesse-Matrix mit eingesetzten kritischen Punkten:
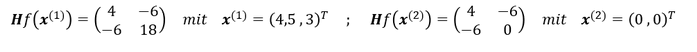
Bestimmung der Definitheit der Hesse-Matrizen mittels Hauptunterdeterminanten-Kriterium:
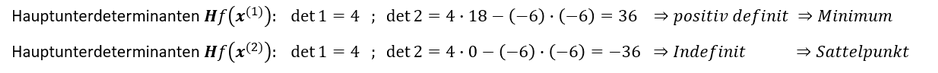
Beim kritischen Punkt 𝒙^((1)) handelt es sich um ein Minimum der Funktion, beim kritischen Punkt 𝒙^((2)) dagegen um einen Sattelpunkt der Funktion.
Video "Definitheit Hesse-Matrix":
Das Probe-Video behandelt die Thematik "Definitheit Hesse-Matrix" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Vertiefung Wirtschaftsmathematik-Paket
Übungen (optional)
20 h Lehrvideos
196 Skriptseiten
Formelsammlung
Klausurlösungen
Live-WebinareDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
