Definitheit - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Vertiefung von Vektoren & Matrizen
Grundlagen der Definitheit einer quadratischen Form:
Für quadratische Formen lassen sich Aussagen über deren Definitheit treffen. Dabei kann eine quadratische Form positiv (semi-)definit, negativ (semi-)definit oder indefinit sein. Die Bestimmung der Definitheit erfolgt dabei über die Matrix 𝑨 der quadratischen Form, wobei die Matrix 𝑨 zunächst in eine symmetrische Matrix umzuwandeln ist. Mittels der symmetrischen Matrix 𝑨 kann dann über die Eigenwerte oder die Hauptunterdeterminanten der Matrix die Definitheit bestimmt werden.
Merke: Die Definitheit von ökonomischen Gleichungen mehrerer Variabler wird vor allem zur Prüfung einer Extremstelle, ob es sich bei dieser um ein Minimum, Maximum oder einen Sattelpunkt handelt, gebraucht.
Methoden zur Bestimmung der Definitheit einer quadratischen Form:
Die Bestimmung der Definitheit einer quadratischen Form kann auf zwei verschiedene Weisen erfolgen:
1. Eigenwerte der Matrix: Durch die Bestimmung der Eigenwerte der symmetrischen Matrix 𝑨 der quadratischen Form lässt sich die Definitheit der quadratischen Form bestimmen.
2. Hauptunterdeterminanten-Kriterium: Durch die Bestimmung der Hauptunterdeterminanten der symmetrischen Matrix 𝑨 der quadratischen Form lässt sich die Definitheit der quadratischen Form bestimmen.
Je nach Wahl der Methode ergibt sich die folgende Definitheit der quadratischen Form:
Video "Definitheit":
Das Probe-Video behandelt die Thematik "Definitheit" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Bestimmung der Definitheit einer quadratischen Form mittels Hauptunterdeterminanten-Kriterium:
Wir wollen die Definitheit der folgenden quadratischen Form mittels des Hauptunterdeterminanten-Kriteriums bestimmen. Dabei unterstellen wir erneut unsere symmetrische Matrix 𝑨, damit das Hauptunterdeterminanten-Kriterium zulässig ist:
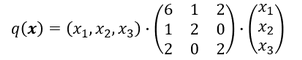
Bestimmung der Hauptunterdeterminanten
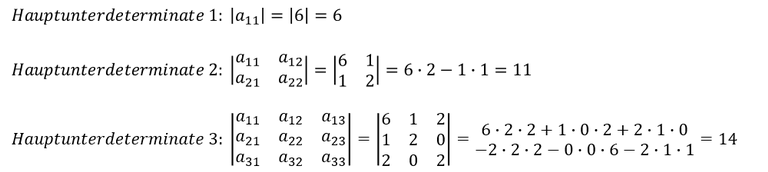
Definitheit
Da alle Hauptunterdeterminanten der symmetrischen Matrix positiv sind, ist die quadratische Form positiv definit.
Nicht-Anwendbarkeit des Hauptunterdeterminanten-Kriteriums: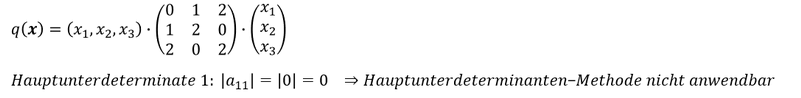
Das Hauptunterdeterminanten-Kriterium ist in einem besonderen Fall nicht anwendbar, nämlich wenn sich die erste Hauptunterdeterminante zu Null ergibt, bzw. der oberste linke Wert der Matrix 𝑨 Null beträgt. In diesem Fall darf die Hauptunterdeterminanten-Methode nicht verwendet werden:
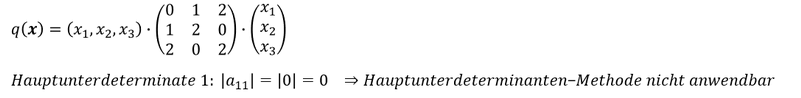
Vertiefung Wirtschaftsmathematik-Paket
196 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)
20 h LehrvideosDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
