Determinante einer Matrix - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Vertiefung von Vektoren & Matrizen
Definition der Determinante:
Die Determinante ist eine reelle Zahl, die sich aus einer quadratischen Matrix (gleiche Anzahl an Zeilen und Spalten) berechnen lässt. Die reelle Zahl lässt sich bei einer 2×2 Matrix als zweidimensionale (𝑅^2 ) Fläche des Parallelogramms der Zeilenvektoren interpretieren. In einer 3×3 Matrix stellt die Determinante das Volumen des dreidimensionalen (𝑅^3 ) Parallelepipeds der Zeilenvektoren dar. Bei quadratischen Matrizen, die eine größere Anzahl an Zeilen/Spalten als 3 besitzen (𝑅^𝑛 ), lässt sich die Determinante hingegen nicht mehr geometrisch veranschaulichen und stellt ein schwer verstehbares axiomatisches Gebäude dar, das aus der Verallgemeinerung der mathematischen Vorgehensweise entsteht.
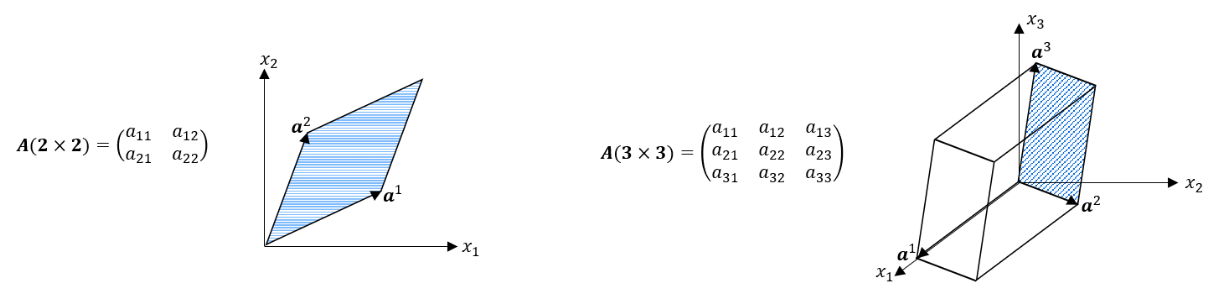
Merke: Es kommt vor allem auf die erfolgreiche Berechnung und Verwendung der Determinante an. Die Interpretation der Determinante ist eher zweitranging.
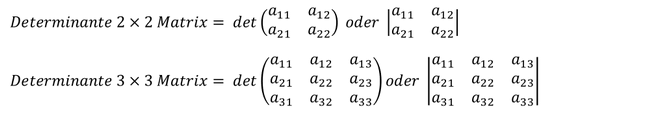
Notation der Determinante:
Die Determinante einer Matrix wird wie folgt notiert bzw. wie folgt bezeichnet:
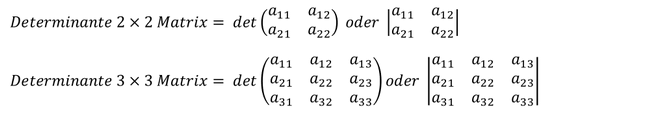
Allgemeine Methoden zur Berechnung einer Determinanten:
Je nach Anzahl der Zeilen/Spalten der Matrix sollten unterschiedliche Methoden zur Berechnung der Determinanten herangezogen werden:
- Regel von Sarrus (nur für 2- und 3-reihige bzw. spaltige Matrizen)
- Laplacescher Entwicklungssatz (meist für 3 oder 4-reihige bzw. spaltige Matrizen)
- Transformation in eine Einheitsmatrix (meist ab 4-reihige bzw. spaltige Matrizen)
Video "Determinante einer Matrix":
Das Probe-Video behandelt die Thematik "Determinante einer Matrix" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Grundlagen der Regel von Sarrus:
Mit der Regel von Sarrus lässt sich die Determinante einer 2- oder 3-reihigen/spaltigen Matrix bestimmen. Die Regel von Sarrus betrachtet dabei die diagonalen Werte einer Matrix und multipliziert diese miteinander. Alle diagonalen Werte von oben links nach unten rechts werden jeweils miteinander multipliziert und addiert. Die „Gegendiagonalen“ von unten links nach oben rechts werden dagegen jeweils multipliziert und vom Ergebnis subtrahiert. Da je nach 2- oder 3-reihiger/spaltiger Matrix eine unterschiedliche Anzahl an Diagonalen existiert, unterscheiden sich die beiden Vorgehensweisen.
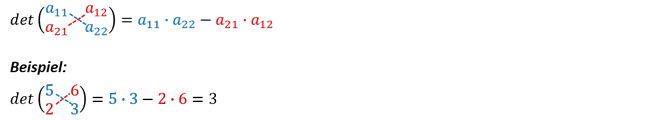
Regel von Sarrus für 𝟐×𝟐 Matrix:
Die Berechnung der Determinanten einer 2×2 Matrix nach der Regel von Sarrus erfolgt, indem man zunächst die diagonalen Werte der Matrix von oben links nach unten rechts miteinander multiplizieren und davon die multiplizierten Werte der Matrix von unten links nach oben rechts abzieht:
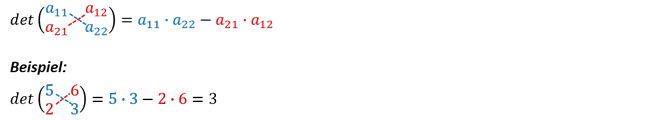
Regel von Sarrus für 𝟑×𝟑 Matrix:
Die Berechnung der Determinanten einer 3×3 Matrix nach der Regel von Sarrus ist etwas komplizierter, denn es gilt zunächst die Matrix um die ersten beiden Spalten zu erweitern, damit genügend Diagonalen gebildet werden können. Die Erweiterung ermöglicht es, in der ersten Zeile insgesamt 3 Diagonalen zu bilden, deren jeweiligen Werte miteinander zu multiplizieren und anschließend zu addieren sind. Davon abzuziehen sind wiederrum die multiplizierten Werte der jeweiligen „Gegendiagonalen“, die sich von unten links nach oben rechts bilden lassen:
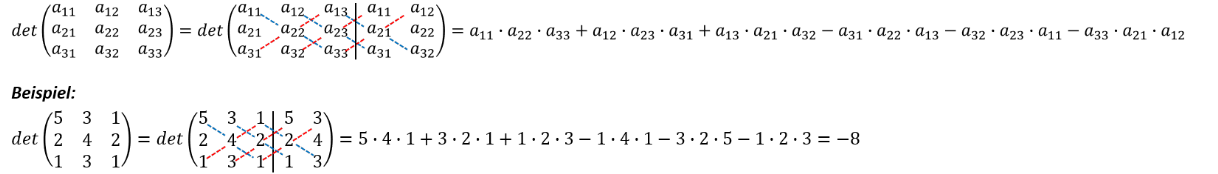
Vertiefung Wirtschaftsmathematik-Paket
Klausurlösungen
Live-Webinare
Übungen (optional)
20 h Lehrvideos
196 Skriptseiten
FormelsammlungDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
