Differentialgleichung - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Differential- und Differenzengleichungen
Definition von Differentialgleichungen:
Eine Differentialgleichung (abgekürzt DGL) ist eine mathematische Gleichung, die eine Beziehung zwischen einer Funktion und ihren Ableitungen darstellt, wobei als Lösung der Differentialgleichung keine reelle Zahl, sondern eine Funktion in Abhängigkeit von einer oder mehreren Variablen gesucht wird. Dabei wird die Funktion in der Differentialgleichung aus Übersichtlichkeitsgründen nicht wie üblich mit 𝑓(𝑥), sondern mit 𝑦(𝑥) oder nur kurz 𝑦 bezeichnet. Die Ableitungen der Funktion werden entsprechend dann meist mit 𝑦′(𝑥), 𝑦^′′ (𝑥), usw. oder nur 𝑦^′, 𝑦^′′, usw. notiert. Anhand einer beispielhaften Differentialgleichung und deren Lösung lässt sich eine Differentialgleichung am leichtesten verstehen.
Beispiel
Es sei die folgende Differentialgleichung (DGL) gegeben:
Als Lösung dieser Differentialgleichung (DGL) ist nun keine reelle Zahl, sondern eine Funktion 𝑦(𝑥) gesucht, wobei die Ableitung dieser Funktion multipliziert mit 4 und abzüglich von 5𝑥 sich zu 0 ergeben muss. Eine entsprechende Funktion und damit die Lösung der Differentialgleichung lautet:
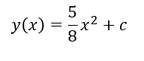
Die Ableitung der Lösungsfunktion der Differentialgleichung eingesetzt in die Differentialgleichung führt nämlich zu 0:
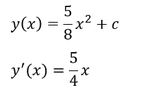
Einsetzen der Ableitung in die Differentialgleichung:
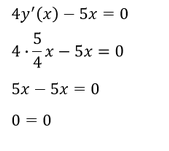
Merke: Bei Differentialgleichungen stellt die Funktion selbst sozusagen eine Variable dar, nach der es aufzulösen gilt, sodass die Differentialgleichung erfüllt wird. Differentialgleichungen treten häufig im Zusammenhang mit Produktion- und Nutzenfunktionen oder Wachstum und Marktprozessen auf.
Grundlagen von Differentialgleichungen mit getrennten Variablen:
Eine Differentialgleichung mit getrennten Variablen ist eine spezielle Differentialgleichung, die sich durch gezieltes Umstellen und Integrieren lösen lässt. Die allgemeine Differentialgleichung mit getrennten Variablen besteht dabei aus zwei Funktionen, die mit 𝑔 und ℎ bezeichnet werden. Die Funktion 𝑔 kann dabei nur von der Variablen 𝑥 und die Funktion ℎ nur von der Variablen 𝑦 abhängig sein, sodass für die Notation der Funktionen in Abhängigkeit ihrer Variablen 𝑔(𝑥) und ℎ(𝑦) gilt. In der DGL mit getrennten Variablen wird die Funktion 𝑔(𝑥) von der Funktion ℎ(𝑦) subtrahiert, oder die Funktion 𝑔(𝑥) steht auf der anderen Seite des Gleichheitszeichens. Die Angabe der Ableitung 𝑦′ in der Differentialgleichung erfolgt bei der Funktion ℎ(𝑦). Entweder wird die erste Ableitung der Funktion 𝑦′ mit der Funktion ℎ(𝑦) multipliziert (𝑦′∙ℎ(𝑦)) oder die Ableitung 𝑦′wird durch die Funktion ℎ(𝑦) dividiert (𝑦^′/ℎ(𝑦) ). Die allgemeine Differentialgleichung mit getrennten Variablen mit den zwei Alternativen lautet folglich:
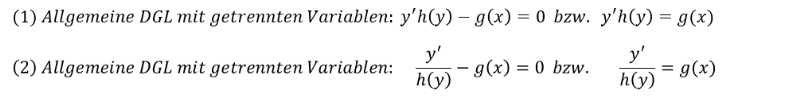
Beispiele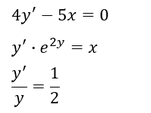
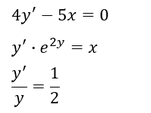
Merke: Die Funktion 𝑔(𝑥) muss nicht zwangsweise die Variable 𝑥 enthalten, die Funktion ℎ(𝑦) dagegen nicht zwangsweise die Variable 𝑦.
Allgemeine Vorgehensweise zur Lösung von Differentialgleichungen mit getrennten Variablen:
Die Lösung einer Differentialgleichung mit getrennten Variablen kann mittels folgender Vorgehensweise erfolgen:
1. Umstellen der Funktion 𝑔(𝑥) auf die rechte Seite der Gleichung (sofern nötig)
2. Umschreiben der Ableitung 𝑦′ in einen Differentialoperator 𝑦^′=𝑑𝑦/𝑑𝑥
3. Äquivalenzumformung mit der Multiplikation von 𝑑𝑥, sodass 𝑑𝑥 auf der rechten Seite der Gleichung mit der Funktion 𝑔(𝑥) multipliziert wird
4. Integrieren beider Seiten, damit 𝑑𝑦 auf der linken und 𝑑𝑥 auf der rechten Seite verschwinden
5. Auflösen der Gleichung nach 𝑦 durch Umformung und Vereinfachung der Konstanten 𝑐_𝑖 zu 𝑐
Video "Differentialgleichung":
Das Probe-Video behandelt die Thematik "Differentialgleichung" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Beispielhafte Lösung einer Differentialgleichungen mit getrennten Variablen bei Multiplikation:
Wir wollen die beispielhaft angegebene Differentialgleichung mit getrennten Variablen bei Multiplikation lösen:
1. Umstellen der Funktion 𝒈(𝒙) auf die rechte Seite der Gleichung (sofern nötig)
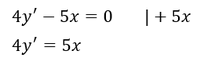
2. Umschreiben der Ableitung 𝒚′ in einen Differentialoperator 𝒚^′=𝒅𝒚/𝒅𝒙
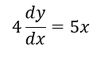
3. Äquivalenzumformung mit der Multiplikation von 𝒅𝒙, sodass 𝒅𝒙 auf der rechten Seite der Gleichung mit der Funktion 𝒈(𝒙) multipliziert wird
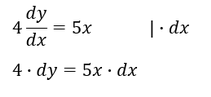
4. Integrieren beider Seiten, damit 𝒅𝒚 auf der linken und 𝒅𝒙 auf der rechten Seite verschwinden
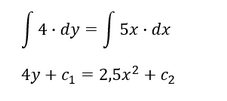
5. Auflösen der Gleichung nach 𝒚 durch Umformung und Vereinfachung der Konstanten 𝒄_𝒊 zu 𝒄
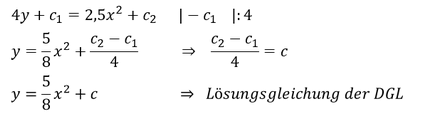
Merke: Ob beliebige Konstanten 𝑐_𝑖 voneinander subtrahiert oder durch einen Wert dividiert werden, das Ergebnis bleibt eine Konstante. Aus diesem Grund lässt sich (𝑐_2−𝑐_1)/4 zu einer Konstanten 𝑐 vereinfachen.
Vertiefung Wirtschaftsmathematik-Paket
Das Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.


