Ecke Polyeder - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Lineare Optimierung
Ecke einer Menge:
Die Ecke einer Menge ist ein wichtiges Spezialelement, denn eine Ecke stellt einen Extrempunkt der Menge dar. Da die Ecke einer Menge mit einem Extrempunkt gleichgesetzt werden kann, werden diese beiden Bezeichnungen oft auch synonym verwendet. Die Ecke einer Menge ist wie folgt definiert:
„ 𝒙 ̅ ist Ecke der Menge 𝑴, wenn 𝒙 ̅ nicht als strenge Konvexkombination 𝒙 ̅ = 𝜆_1 𝒙^𝟏 + 𝜆_2 𝒙^𝟐 für zwei verschiedene Punkte 𝒙^𝟏, 𝒙^𝟐 aus 𝑴 geschrieben werden kann. Strenge Konvexkombination heißt hierbei 𝜆_𝑖 ≠ 𝟎 für 𝒊 = 𝟏,𝟐 (und damit auch 𝜆_𝑖 ≠ 𝟏) “
Ein bestimmter Punkt einer Menge ist also genau dann eine Ecke, wenn es nicht möglich ist, diesen Punkt über eine verbindende Strecke für je zwei gewählte Punkte 𝑥^1 und 𝑥^2 aus der Teilmenge 𝑀 darzustellen. Die folgenden Grafiken sollen die Definition einer Ecke noch einmal veranschaulichen:
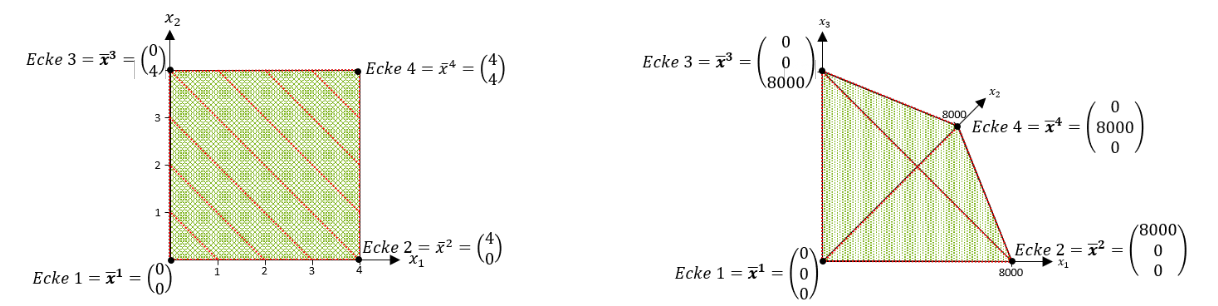
Jeder Randpunkt der Menge könnte durch eine Konvexkombinationen der Ecken 1, 2, 3 oder 4 dargestellt werden. Jeglicher Punkt innerhalb der Menge könnte durch eine Konvexkombination der Ecken oder Randpunkte dargestellt werden. Nur die Ecken selbst können nicht durch eine Konvexkombination dargestellt werden, wenn 𝜆_𝑖 ≠ 0 bzw. 𝜆_𝑖 ≠ 1 gewählt werden muss (strenge Konvexkombination). Denn für die Ecken gibt es keine Punkte, die man innerhalb der Teilmenge wählen kann, dass die Ecken auf einer Verbindungslinie zwischen diesen beiden Punkten liegen.
Ecken von Polyedern des 𝑹^𝒏:
Der Zulässigkeitsbereich der Lösung eines linearen Optimierungsmodells wird durch seine begrenzenden Nebenbedingungen 𝒂^𝒊𝑻∙𝒙 ≤ 𝑏_𝑖 definiert. Als Mengentyp stellt der Zulässigkeitsbereich dabei ein Polyeder dar. Aus der Definition der Ecke einer Menge, lässt sich für die Ecken eines Polyeders folgendes ableiten:
„Ecken von Polyedern des 𝑹^𝒏 liegen genau dort, wo sich 𝒏 oder mehr Hyperebenen 𝒂^𝒊𝑻∙𝒙 = 𝑏_𝑖 der das Polyeder bildenden Halbräume 𝒂^𝒊𝑻∙𝒙 ≤ 𝑏_𝑖 schneiden, niemals weniger!“
Folglich muss bei einem 𝑹^𝟐 sowohl die 𝑥_1 als auch die 𝑥_2-Ebene durch eine oder mehrere Nebenbedingungen begrenzt werden, damit eine Ecke im Zulässigkeitsbereich entsteht. Für ein 𝑹^𝟑 muss sowohl die 𝑥_1, 𝑥_2 als auch die 𝑥_3-Ebene durch eine oder mehrere Nebenbedingungen begrenzt werden, damit eine Ecke im Zulässigkeitsbereich entsteht.
Video "Ecke von Polyeder":
Das Probe-Video behandelt die Thematik "Ecke von Polyeder" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Vertiefung Wirtschaftsmathematik-Paket
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)
20 h Lehrvideos
196 SkriptseitenDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
