Eigenwerte einer Matrix - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Vertiefung von Vektoren & Matrizen
Grundlagen der Berechnung der Eigenwerte einer Matrix:
Die Eigenwerte einer Matrix können direkt berechnet werden, wobei eine Matrix meist nicht nur einen, sondern mehrere Eigenwerte besitzt. Die Berechnung der Eigenwerte erfolgt dabei über das sogenannte charakteristische Polynom, dessen Nullstellen ermittelt werden müssen.
Charakteristisches Polynom einer Matrix:
Um zum charakteristischen Polynom einer Matrix 𝑨 zu gelangen, ist von den diagonalen Werten einer Matrix die allgemeine Bezeichnung für den Eigenwert 𝜆 abzuziehen. Nach dieser Anpassung stellt die Determinante dieser Matrix das charakteristische Polynom dar. Es soll zunächst allgemein die Bildung des charakteristischen Polynoms für eine 2×2 und 3×3-Matrix dargestellt werden, wobei 𝑰 eine Einheitsmatrix bzw. die Diagonale der Matrix darstellt:
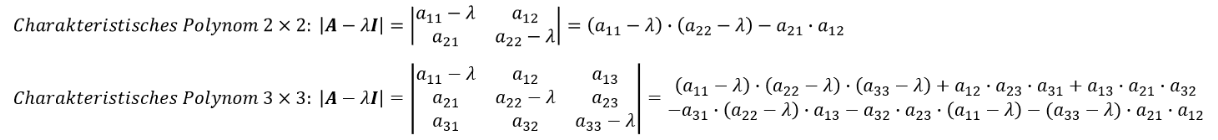
Allgemeine Berechnung der Eigenwerte: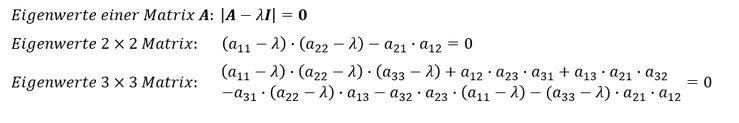
Die Eigenwerte einer Matrix entsprechen den Nullstellen des charakteristischen Polynoms. Folglich gilt es das charakteristische Polynom gleich 0 zu setzen und alle Nullstellen der Gleichung zu ermitteln. Die verschiedenen Nullstellen des Polynoms stellen dann die Eigenwerte der Matrix dar:
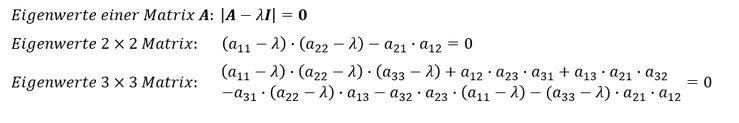
Merke: Da das charakteristische Polynom eine Funktion 𝑛-ten Grades ist, können maximal 𝑛 Nullstellen auftreten. Die Bestimmung von Nullstellen einer Funktion 2. Grades kann noch relativ einfach mit Hilfe der PQ-Formel vollzogen werden. Bei einer Funktion 3. Grades kann man sich bei den Eigenwerten eines Tricks behelfen, sodass eine Polynomdivision zur eindeutigen Bestimmung der Nullstellen nicht zwingend notwendig ist. Die Nullstellen von Funktionen größer als 3. Grades können nur sehr schwierig und mit mathematisch komplexen Systemen bestimmt werden.
Rechenbeispiel für die Eigenwerte einer 𝟐×𝟐-Matrix:
Es sollen die Eigenwerte der folgenden Matrix 𝑨 berechnet werden: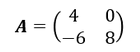
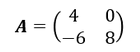
Charakteristisches Polynom der Matrix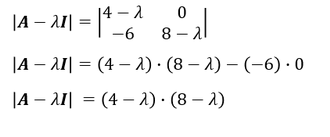
Die Diagonale der Matrix ist mit der Subtraktion von 𝜆 zu ergänzen. Nach der Ergänzung gilt es die Determinante zu berechnen:
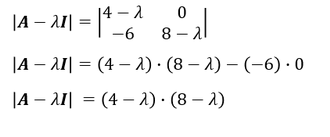
Eigenwerte der Matrix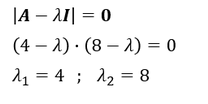
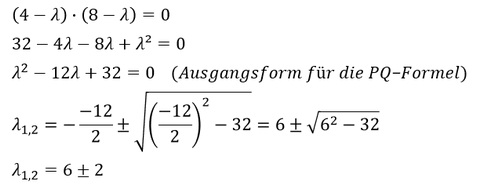
Das charakteristische Polynom der Matrix ist gleich 0 zu setzen. Es gilt die Nullstellen für 𝜆 zu ermitteln:
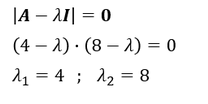
Merke: Die Eigenwerte der Matrix 𝑨 können direkt ermittelt werden. Für 𝜆_1 kann der Wert gewählt werden, der die linke Klammer und damit die ganze Multiplikation zu 0 werden lässt. Für 𝜆_2 kann der Wert gewählt werden, der die rechte Klammer und damit die ganze Multiplikation zu 0 werden lässt. Alternativ wäre aber auch eine Lösung über die PQ-Formel möglich gewesen.
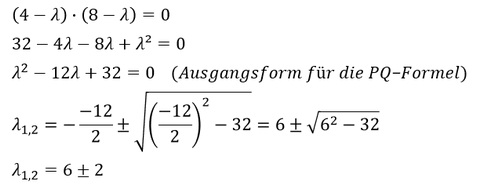
Video "Eigenwerte einer Matrix":
Das Probe-Video behandelt die Thematik "Eigenwerte einer Matrix" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Rechenbeispiel für die Eigenwerte einer 𝟑×𝟑-Matrix:
Es sollen die Eigenwerte der folgenden Matrix 𝑨 berechnet werden: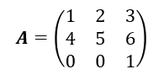
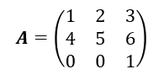
Charakteristisches Polynom der Matrix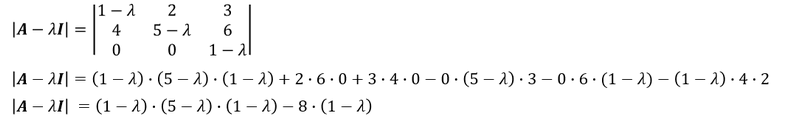
Die Diagonale der Matrix ist mit der Subtraktion von 𝜆 zu ergänzen. Nach der Ergänzung gilt es die Determinante zu berechnen:
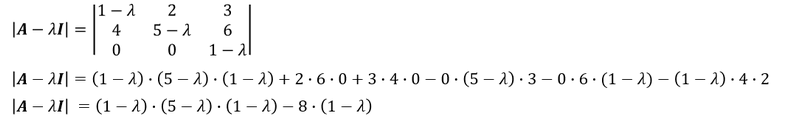
Eigenwerte der Matrix
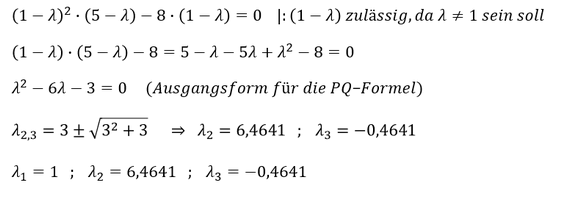
Das charakteristische Polynom der Matrix ist gleich 0 zu setzen. Es gilt die Nullstellen für 𝜆 zu ermitteln:
Achtung: Da mit 𝜆_1=1 bereits ein Eigenwert bestimmt ist, gilt für die anderen Eigenwerte, dass sie ungleich dieses Eigenwerts sein müssen λ≠1. Diese Tatsache erlaubt es uns, die Funktion des charakteristischen Polynoms durch (1-𝜆) zu dividieren, sodass eine Funktion 2. Grades entsteht, die mit der PQ-Formel zu lösen ist. Dieser Trick ermöglicht es uns also, die langwierige Prozedur einer Polynomdivision zu umgehen.
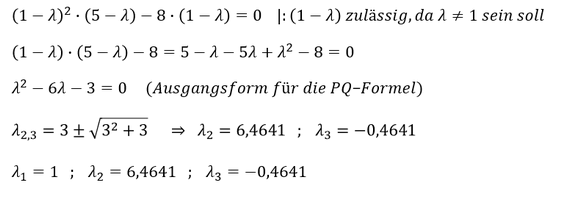
Vertiefung Wirtschaftsmathematik-Paket
Live-Webinare
Übungen (optional)
20 h Lehrvideos
196 Skriptseiten
Formelsammlung
KlausurlösungenDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
