Elastizitätsmatrix - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Vertiefung der Differentialrechnung
Nachfragefunktionen mehrerer Variabler: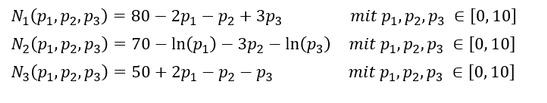
Die klassische Nachfragefunktion beschreibt die nachgefragte Menge eines Gutes in Abhängigkeit des Preises dieses Gutes (𝑁(𝑝)). Es gibt jedoch auch Nachfragefunktionen von Gütern, deren nachgefragte Menge nicht nur vom Preis des betrachteten Gutes, sondern auch von den Preisen anderer Güter abhängig ist (𝑁_1 (𝑝_1, 𝑝_2,…,𝑝_𝑛)). Solche Nachfragefunktionen treten am häufigsten bei Komplementärgütern (Güter die gemeinsam nachgefragt werden, weil sie sich in ihrem Nutzen ergänzen) oder Substitutionsgütern (Güter die dieselben oder ähnliche Bedürfnisse stillen und deshalb andere Güter ersetzen können) auf. Es gilt dabei zu beachten, dass eine Nachfragefunktion 𝑁 immer nur die Nachfrage für ein Gut 𝑖 angibt und dieses Gut nur einen Preis 𝑝_𝑖 besitzen kann, wobei Nachfrage und der Preis des Gutes durch den gleichen Index bzw. durch das gleiche Gut 𝑖 gekennzeichnet sind. Im Falle mehrerer Preise 𝑝_𝑖 muss es folglich auch mehrere Nachfragefunktionen 𝑁_𝑖 der einzelnen Güter 𝑖 geben. Die folgenden beispielhaften Nachfragefunktionen mehrerer Variabler sollen die Zusammenhänge veranschaulichen:
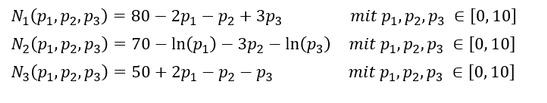
Definition der direkten Preiselastizität:
Die direkte Preiselastizität beschreibt die relative Veränderung der Nachfrage eines Gutes, wenn der Preis dieses Gutes relativ (1%) verändert wird. Folglich entspricht die direkte Preiselastizität der partiellen Elastizität der Nachfragefunktion nach dem Preis, der für das Gut der Nachfragefunktion gilt. Wir wollen die direkten Preiselastizitäten der angegebenen Nachfragefunktionen ermitteln:
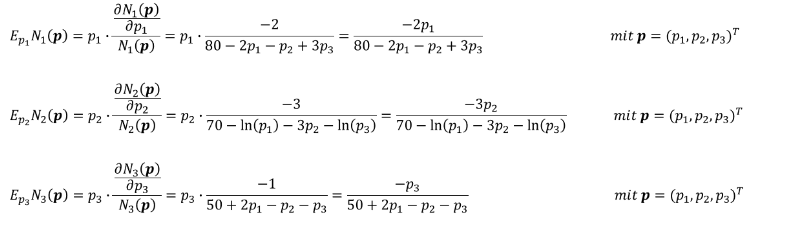
Merke: Direkte Preiselastizitäten geben die relativen Veränderungen ihrer nachgefragten Menge nach dem entsprechenden Gut an, wenn der Preis eben dieses Gutes um 1% erhöht, jedoch die Preise der anderen Güter konstant gehalten wurden.
Definition der Kreuzelastizität:
Die Kreuzelastizität beschreibt die relative Veränderung der Nachfrage eines Gutes, wenn der Preis eines anderen Gutes relativ (1%) verändert wurde, von dem die Nachfragefunktion des Gutes abhängig ist. Folglich entspricht die Kreuzelastizität der partiellen Elastizität der Nachfragefunktion nach einem abhängigen Preis, der nicht für das Gut der Nachfragefunktion gilt. Zum besseren Verständnis wollen wir die Kreuzelastizitäten der uns von der vorherigen Folie bekannten Nachfragefunktionen ermitteln:

Video "Elastizitätsmatrix":
Das Probe-Video behandelt die Thematik "Elastizitätsmatrix" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Elastizitätenmatrix mehrerer (Nachfrage-)Funktionen:
Die Elastizitätenmatrix mehrerer reeller Funktionen 𝑓_𝑖 (𝑥_1, 𝑥_2,…, 𝑥_𝑛 ) ist eine Matrix, die alle direkten Elastizitäten und Kreuzelastizitäten der einzelnen Funktionen 𝑓_1,𝑓_2,…𝑓_𝑚 enthält. Analog dazu gilt für eine Elastizitätenmatrix mehrerer Nachfragefunktionen 𝑁_𝑖 (𝑝_1, 𝑝_2,…,𝑝_𝑛), dass sie alle direkten Preiselastizitäten und Kreuzelastizitäten der einzelnen Nachfragefunktionen 𝑁_1,𝑁_2,…𝑁_𝑚 enthält. Allgemein lässt sich die Elastizitätenmatrix für reelle Funktion 𝑓_𝑖 bzw. für Nachfragefunktionen 𝑁_𝑖 wie folgt darstellen:
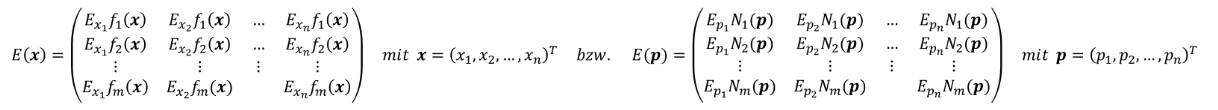
Merke: Die einzelnen Zeilen der Elastizitätenmatrix gelten den verschiedenen (Nachfrage-)Funktionen. Die einzelnen Spalten der Elastizitätenmatrix gelten dagegen den relativen Veränderungen der 𝑥_𝑖-Werte bzw. der Preise 𝑝_𝑖. Um sich den Aufbau der Elastizitätenmatrix besser merken zu können, kann man sich die Elastizitätenmatrix wie eine Tabelle vorstellen, die in der Vorspalte die (Nachfrage-)Funktionen und in der Kopfzeile das Symbol der Elastizität mit der relativ veränderten Variablen (𝑥_𝑖 oder 𝑝_𝑖) der Reihenfolge nach enthält. Die Kombinationen ergeben sich dann zu den verschiedenen direkten Elastizitäten und Kreuzelastizitäten, wobei darauf zu achten ist, dass die Kopfzeile zuerst zu notieren ist:
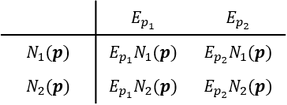
Beispielhafte Darstellung einer Elastizitätenmatrix: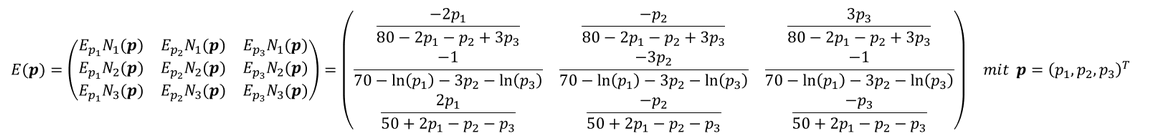
Die Elastizitätenmatrix soll mit unseren bereits berechneten direkten Preiselastizitäten und Kreuzelastizitäten der vorherigen Folien veranschaulicht werden:
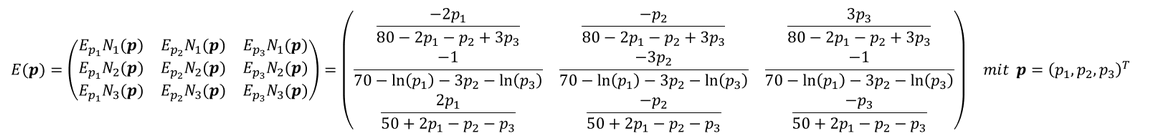
Merke: Die Diagonale der Elastizitätenmatrix enthält die direkten Preiselastizitäten.
Vertiefung Wirtschaftsmathematik-Paket
Das Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.


