Homogenitätsgrad - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Vertiefung der Differentialrechnung
Homogenität von Funktionen mehrerer Variabler:
Die Eigenschaft der Homogenität einer Funktion ist vor allem für die Ökonomie von Bedeutung. Die Homogenität beschreibt dabei die Veränderung des Funktionswertes bei einer beliebig gleichen Vervielfachung der abhängigen Variablen. Da vor allem Funktionen mehrerer Variabler ökonomisch relevant sind, soll im Folgenden die allgemeine Bestimmung der Homogenität und des damit einhergehenden Homogenitätsgrads einer ökonomischen Funktion mehrerer Variablen veranschaulicht werden.
Allgemeine Ermittlung der Homogenität einer Funktion mehrerer Variabler:
Um zu überprüfen, ob es sich bei der gegebenen nicht-linearen Funktion mehrerer Variabler um eine homogene Funktion handelt, ist jede Variable der Funktion um einen Faktor 𝜆 zu erhöhen. Sofern es möglich ist, diesen Faktor für alle Terme der Funktion auszuklammern, sodass die Funktion in der Klammer wieder für sich selbst steht, ist die Funktion homogen. Die Bestimmung der Homogenität soll beispielhaft mittels folgender nicht-linearer Funktion veranschaulicht werden:
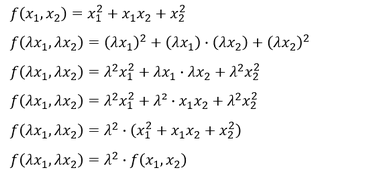
Die Funktion ist homogen, da eine Vervielfachung der Variablen um den gleichen Faktor 𝜆 zu einer 𝜆^2 Vervielfachung des Funktionswertes führt.
Achtung: Lässt sich der Faktor 𝜆 nicht für alle Terme der Funktion ausklammern, sodass die Funktion nicht wieder für sich selbst steht, ist die Funktion inhomogen.
Homogenitätsgrad einer Funktion mehrerer Variabler:
Der Homogenitätsgrad der Funktion entspricht dem Exponenten des ausgeklammerten Faktors 𝜆, wobei der Exponent allgemein mit 𝛼 (𝜆^𝛼) notiert wird. Je nach Wert des Exponenten des ausgeklammerten Faktors 𝜆 spricht man von einer linearen-, überlinearen- oder unterlinearen-homogenen Funktion:
Linear-homogene Funktion: 𝛼 = 1 𝑏𝑧𝑤. 𝜆^(𝛼=1)
Überlinear-homogene Funktion: 𝛼 > 1 𝑏𝑧𝑤. 𝜆^(𝛼>1)
Unterlinear-homogene Funktion: 𝛼 < 1 𝑏𝑧𝑤. 𝜆^(𝛼<1)
Merke: Die nicht-lineare Funktion in unserem Beispiel ist folglich überlinear-homogen, denn sie besitzt einen Homogenitätsgrad von 2: 𝑓(𝜆𝑥_1, 𝜆𝑥_2 ) = 𝜆^2 ∙ 𝑓(𝑥_1, 𝑥_2 )
Video "Homogenitätsgrad":
Das Probe-Video behandelt die Thematik "Homogenitätsgrad" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Rechenbeispiel einer homogenen Funktion mit Beweisführung:
Wir wollen die folgende nicht-lineare Funktion mehrerer Variabler auf Homogenität überprüfen und den Homogenitätsgrad bestimmen. Danach soll noch ein Beweis erfolgen, dass sich der Funktionswert bei Erhöhung der Variablen um den Faktor 𝜆 tatsächlich um den berechneten Faktor 𝜆^𝛼 verändert: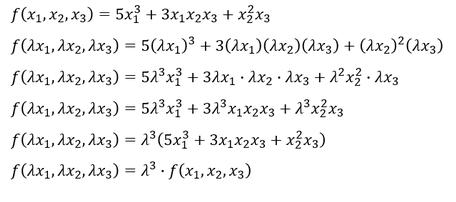
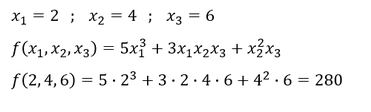
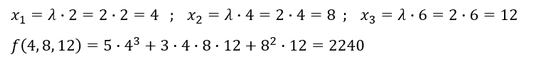
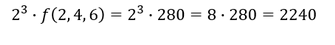
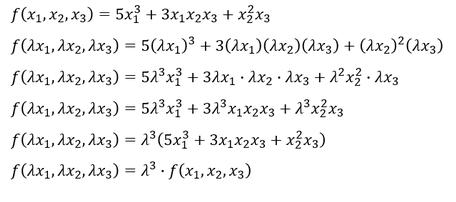
Die Funktion ist homogen vom Grad 3. Eine Erhöhung aller Variablen um den beliebig wählbaren Faktor 𝜆 führt zu einer 𝜆^3-fachen Veränderung des Funktionswertes. Zum Beweis wollen wir zunächst den Funktionswert ausrechnen, wenn für die Variablen folgende Werte gelten:
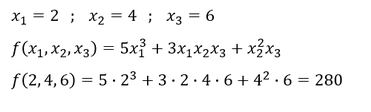
Nun sollen die einzelnen Variablen um den Faktor 𝜆=2 erhöht werden, bzw. es soll der Wert jeder Variablen verdoppelt werden. Es ergibt sich folgender Funktionswert nach der Veränderung der Variablen um den Faktor 𝜆=2:
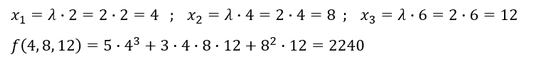
Der Funktionswert ergibt sich nach der Verdopplung der Variablen zu 2240. Der gleiche Wert hätte sich allerdings auch ergeben, wenn wir den Funktionswert von 280 mit 𝜆^3 bzw. 2^3 multipliziert hätten:
Bei Bekanntheit der Homogenität und dessen Grad kann folglich auf eine erneute Berechnung des Funktionswertes mit dem Vielfachen der Variablen verzichtet werden.
Merke: Die Homogenität ist vor allem für Produktionsfunktionen von essenzieller Bedeutung. Mit dem Homogenitätsgrad kann sofort bestimmt werden, wie sich der Output verändert, wenn beispielsweise die doppelte Menge an Inputfaktoren verwendet wird.
Vertiefung Wirtschaftsmathematik-Paket
Live-Webinare
Übungen (optional)
20 h Lehrvideos
196 Skriptseiten
Formelsammlung
KlausurlösungenDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
