Lagrange Verfahren - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Extrema nicht-linearer Funktionen
Beispielhafte Bestimmung der Lösung eines nicht-linearen Optimierungsproblems mittels Lagrange-Funktion: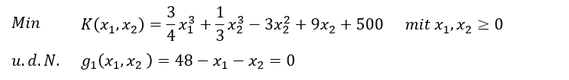
Wir wollen die optimale Lösung des uns bereits bekannten Optimierungsproblems mittels Lagrange-Funktion der folgenden Aufgabe ermitteln:
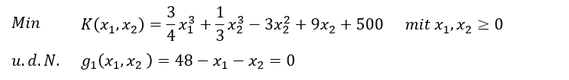
Anwendung des Verfahrens der Lagrange-Funktion:
1. Aufstellen der Lagrange-Funktion
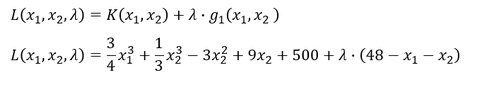
2. Partielles Ableiten nach allen Variablen der Lagrange-Funktion und Nullsetzen (Bedingungen erster Ordnung)
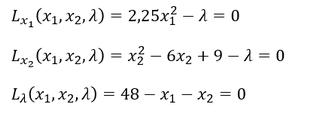
3. Variablen der partiellen Ableitungen als gemeinsames Gleichungssystem lösen (Einsetzverfahren, Ausklammern, oder Methoden zur Lösung von Gleichungssystemen)
Wir wollen das Einsetzverfahren verwenden, indem wir zunächst die partielle Ableitung 𝐿_𝜆 nach 𝑥_1 umstellen und die Gleichung in die partielle Ableitung 𝐿_(𝑥_1 ) einsetzen. Die partielle Ableitung 𝐿_(𝑥_1 ) gilt es dann nach 𝜆 umzustellen und in die partielle Ableitung 𝐿_(𝑥_2 ) einzusetzen, damit eindeutig nach 𝑥_2 aufgelöst werden kann. Die Ermittlung der anderen Variablen erfolgt dann durch rekursives Einsetzen in die vorherigen umgestellten Gleichungen. Andere Vorgehensweisen zur Lösung wären natürlich auch möglich.
- Partielle Ableitung 𝐿_𝜆 nach 𝑥_1 umstellen:
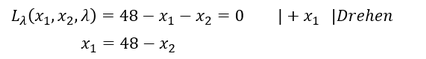
- Einsetzen der umgestellten partiellen Ableitung 𝑥_1=48−𝑥_2 in die partielle Ableitung 𝐿_(𝑥_1 ) und Auflösen nach 𝜆:
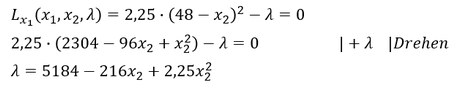
- Einsetzen der umgestellten partiellen Ableitung 𝜆=5184−216𝑥_2+2,25𝑥_2^2 in die partielle Ableitung 𝐿_(𝑥_2 ) und Auflösen nach 𝑥_2:
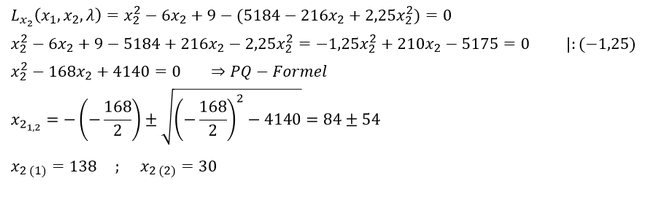
- Rekursives Einsetzen der Lösung in die vorherigen Gleichungen:
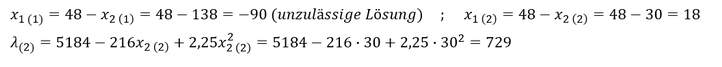
Da die Variablen 𝑥_1 und 𝑥_2 nur positive Werte annehmen dürfen, ist nur die gefundene Extremstelle 𝑥_1=18 und 𝑥_2=30 zur Lösung des Optimierungsproblems zulässig.
4. Prüfung auf Minimum/Maximum und Berechnung des optimalen Zielfunktionswertes (optional)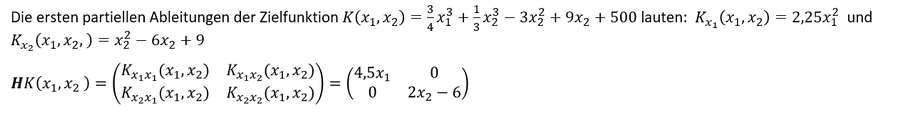
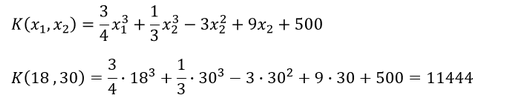
Bei der optimalen Lösung der Lagrange-Funktion handelt es sich um einen kritischen Punkt, der unter gewissen Umständen mittels der Definitheit der Hesse-Matrix der Zielfunktion des nicht-linearen Optimierungsmodells überprüft werden kann, ob es sich dabei um ein Minimum, Maximum oder einen Sattelpunkt handelt. Sofern sich allerdings kein Extremum über die Hesse-Matrix ergibt, muss auf das Verfahren der Variablensubstitution und dessen Prüfung auf ein Extremum zurückgegriffen werden.
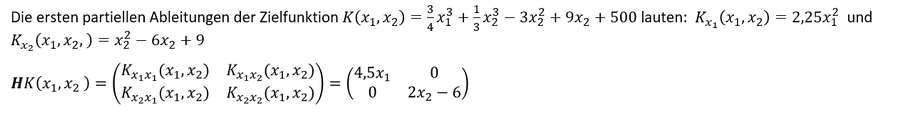
Einsetzten des kritischen Punktes 𝑥_1=18 und 𝑥_2=30
Da die Definitheit der Hesse-Matrix der Zielfunktion für die optimale Lösung positiv ist, handelt es sich bei der optimalen Lösung um ein Minimum.
Die Höhe der Kosten im Minimum lassen sich durch einsetzten der optimalen Lösung in die Kostenfunktion berechnen:
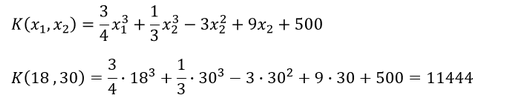
Die Kosten im Minimum ergeben sich zu 11444 GE.
Merke: Der berechnete Lagrange-Multiplikator 𝜆=729 trifft eine Aussage darüber, wie sich die Kosten im Minimum annähernd verändern würden, wenn der begrenzende Wert der Nebenbedingung um eine Einheit steigt bzw. wenn als Nebenbedingung 〖49−𝑥〗_1−𝑥_2=0 gelten würde.
Video "Lagrange Verfahren":
Das Probe-Video behandelt die Thematik "Lagrange Verfahren" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Vertiefung Wirtschaftsmathematik-Paket
20 h Lehrvideos
196 Skriptseiten
Formelsammlung
Klausurlösungen
Live-Webinare
Übungen (optional)Das Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
