Simplex-Tableau - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Lineare Optimierung
Allgemeine Aufstellung eines Simplextableaus:
Zur allgemeinen Aufstellung eines Simplextableaus für ein lineares Optimierungsmodell gilt es zunächst die Zielfunktion als zusätzliche Nebenbedingung zu formulieren. Danach sind die echten Nebenbedingungen um ihre Schlupfvariablen zu ergänzen. Das angepasste lineare Optimierungsmodell gilt es dann in Matrix-Schreibweise zu notieren und die Matrix und einzelnen Vektoren in eine sogenannte Kreuzform einzusortieren. Die einzelnen Schritte sollen nacheinander beschrieben werden:
Formulierung der Zielfunktion als Nebenbedingung
Um die Zielfunktion als Nebenbedingung zu formulieren, ist zunächst der Zielfunktionsfunktionswert 𝑧 mit 𝑥_0 zu ersetzen. Zusätzlich soll der Zielfunktionswert auf null lauten, da wir davon ausgehen, dass zunächst keinerlei Produktion erfolgt (Startpunkt im Ursprung des Koordinatensystems). Die Zielfunktion gilt es folgend wie eine Nebenbedingung umzustellen, dass alle Variablen gemeinsam auf der linken Seite der Funktion stehen. Wir wollen von unserer bekannten Zielfunktion ausgehen:

Ergänzung der echten Nebenbedingungen um Schlupfvariablen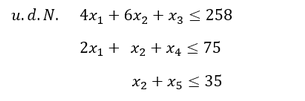
Für jede echte Nebenbedingung ist durch Addition eine Schlupfvariable 𝑥_𝑖 einzuführen. Wir wollen von den uns bekannten Nebenbedingungen ausgehen:
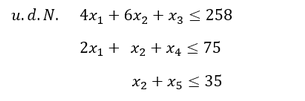
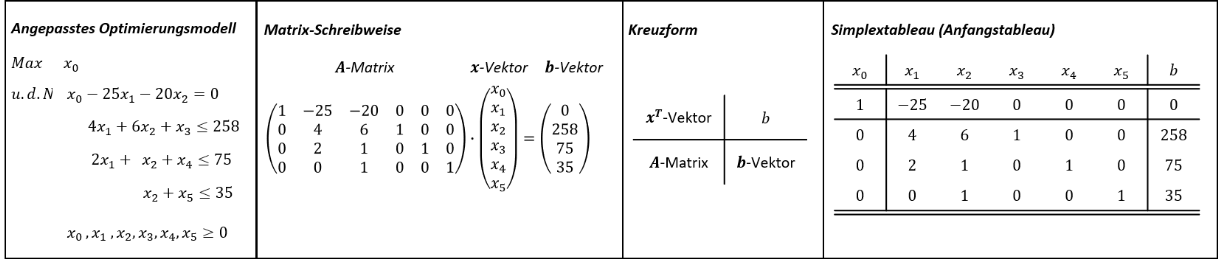
Allgemeines vereinfachtes Aufstellen eines Simplextableaus:
Die Aufstellung eines Simplextableaus muss nicht unbedingt in den mathematischen Schritten über die Matrixschreibweise erfolgen. Mit dem Verständnis, wie ein Simplextableau allgemein aufgestellt wird, kann das Aufstellen des Simplextableaus auch direkt aus dem unveränderten linearen Optimierungsmodell erfolgen. Dazu sind folgende Schritte notwendig, wobei wir das folgende neue lineare Optimierungsmodell unterstellen wollen:
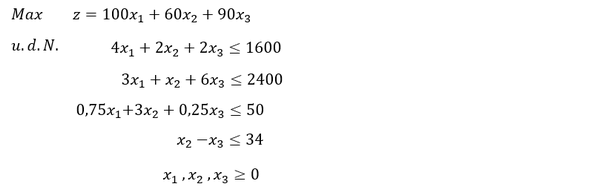
Schritt 1: Aufstellen der allgemeinen Variablenzeile des Simplextableaus
Als erstes sollte mit der Notation der allgemeinen Variablenzeile des Simplextableaus begonnen werden, die alle Variablen des Tableaus angibt. Dazu gilt es zunächst 𝑥_0 für die Zielfunktion zu notieren. Danach folgen die 𝑥_𝑖-Variablen des linearen Optimierungsmodells. Ergänzend zu diesen Variablen sind zusätzliche Schlupfvariablen in Höhe der Anzahl an Nebenbedingungen entweder mit fortlaufendem 𝑥_𝑖 oder mit 𝑠_𝑖 zu notieren. Als letzte Variable gilt es den kleinen Buchstaben „𝑏“ zu notieren. Nach der Notation aller Variablen ist sowohl die erste Variable 𝑥_0 als auch der Buchstabe 𝑏 durch einen Senkrechtstrich abzugrenzen und ein Doppelstrich unter die erste Zeile zu zeichnen:

Schritt 2: Notieren der ersten Zeile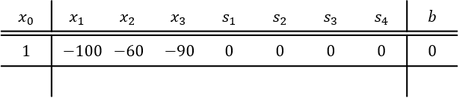
Es ist die erste Zeile zu notieren, wobei für 𝑥_0 der Wert 1 einzutragen ist. Die restlichen reellen Zahlen die für die jeweilige 𝑥_𝑖-Variable gelten, lassen sich der Zielfunktion entnehmen, wobei diese mit umgekehrtem Vorzeichen zu notieren sind. Für die restlichen Variablen, die nicht in der Zielfunktion vorkommen, als auch 𝑏, gilt der Wert 0. Anschließend ist unter die komplette erste Zeile ein Strich zu ziehen:

Schritt 3: Notieren aller Nebenbedingungen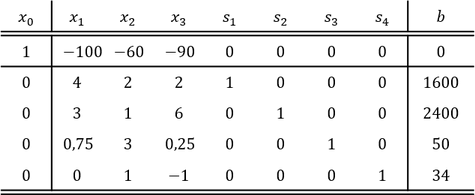
Als letzten Schritt gilt es alle Nebenbedingungen passend untereinander in das Simplextableau einzutragen. Dazu sind die reellen Zahlen vor den 𝑥_𝑖-Variablen der Nebenbedingungen für die passende 𝑥_𝑖-Spalte zeilenweise zu notieren. Zusätzlich muss für jede Nebenbedingung je eine Schlupfvariable den Wert 1 erhalten, wobei dies der Reihenfolge nach geschehen sollte. Das bedeutet die erste Nebenbedingung erhält bei der Schlupfvariablen 𝑠_1 den Wert 1, die zweite Nebenbedingung erhält bei der Schlupfvariablen 𝑠_2 den Wert 1, usw.. Variablen die nicht in der Nebenbedingung vorkommen sind mit dem Wert 0 zu notieren:

Merke: Bei der ersten Spalte des Simplextableaus handelt es sich bei dieser Schreibweise immer um einen Einheitsvektor, da 𝑥_0 ausschließlich in der Zielfunktion vorkommt. Die Schlupfvariablen bilden dagegen, wenn man nur die Zeilen der Nebenbedingungen betrachtet, immer eine Einheitsmatrix ab.
Video "Simplex-Tableau":
Das Probe-Video behandelt die Thematik "Simplex-Tableau" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Vertiefung Wirtschaftsmathematik-Paket
Das Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.


