Simplex Verfahren - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Lineare Optimierung
Allgemeine Vorgehensweise zur Bestimmung der optimalen Basislösung:
Das Ziel des Simplex-Algorithmus ist es, die optimale Lösung für das lineare Optimierungsmodell zu liefern. Um zu dieser optimalen Lösung zu gelangen, ist das Simplextableau des Simplex-Algorithmus durch Pivot-Schritte solange zu verändern, bis der Zielfunktionswert nicht mehr durch einen weiteren Pivot-Schritt erhöht werden kann. In diesem Fall stellt die zulässige Basislösung des Simplextableaus auch gleichzeitig die optimale (Basis)Lösung für das lineare Optimierungsmodell dar. Die allgemeine Vorgehensweise um zur optimalen Basislösung zu gelangen, lässt sich in die folgenden 5 wiederholbaren Schritte unterteilen:
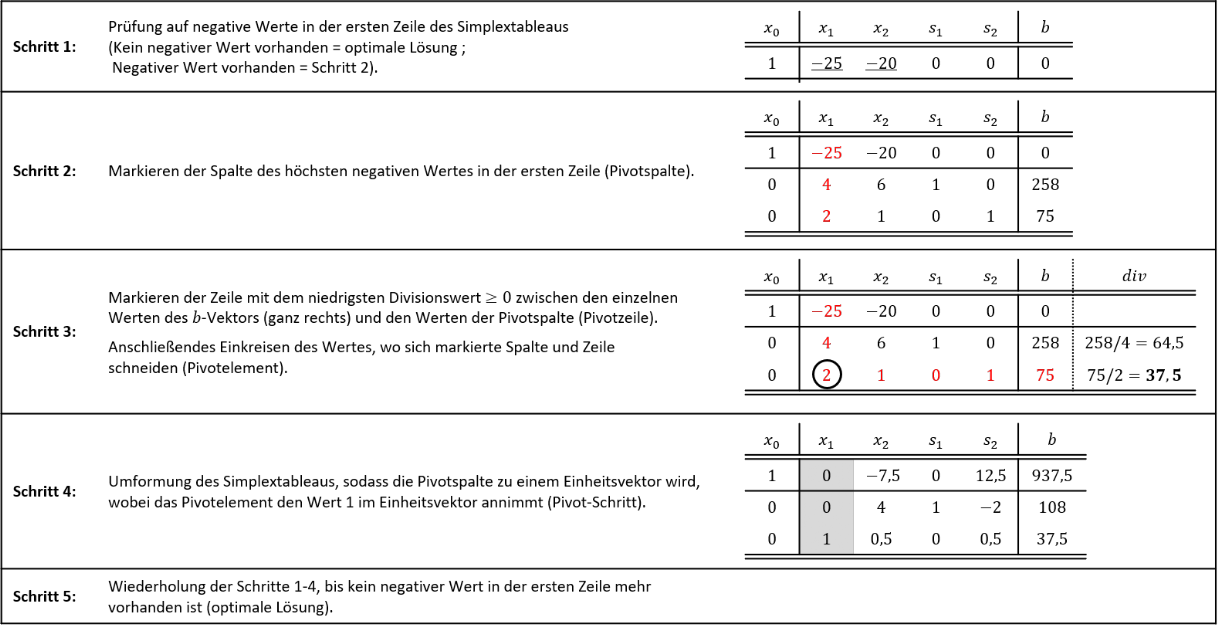
Allgemeine mathematische Durchführung eines Pivot-Schritts:
Bei der mathematischen Durchführung eines Pivot-Schritts wird das Simplextableau so umgeformt, dass die Pivotspalte einem Einheitsvektor entspricht. Alle Werte der Pivotspalte sind folglich zu Nullen umzuformen, bis auf das Pivotelement, das den Wert „1“ annimmt. Die Umformung selbst vollzieht sich dabei durch die Subtraktion eines jeweiligen Vielfachen der Pivotzeile von den jeweiligen anderen Zeilen des Simplextableaus. Die Pivotzeile selbst wird dagegen durch den Wert des Pivotelements dividiert. Allgemein kann zur mathematischen Durchführung eines Pivot-Schritts wie folgt vorgegangen werden:
1. Ergänzung des Simplextableaus um eine weitere Spalte in der die Rechenwege der folgenden Punkte zur nötigen Umformung notiert werden
2. Notieren der Subtraktionen der jeweiligen Zeilen abzüglich der Pivotzeile, wobei die Zeilen mit römisch 𝐼, 𝐼𝐼, 𝐼𝐼𝐼, 𝐼𝑉, usw. benannt werden
3. Ergänzung eines jeweiligen Multiplikators für die abzuziehende Pivotzeile, wobei der jeweilige Multiplikator ein Bruch ist, mit dem Wert der Pivotspalte in dieser Zeile als Zähler und dem Wert des Pivotelements als Nenner
4. Notieren der Division der Pivotzeile durch den Wert des Pivotelements
5. Durchführung der notierten Rechenwege in der ergänzten Spalte mit jedem Wert des Simplextableaus
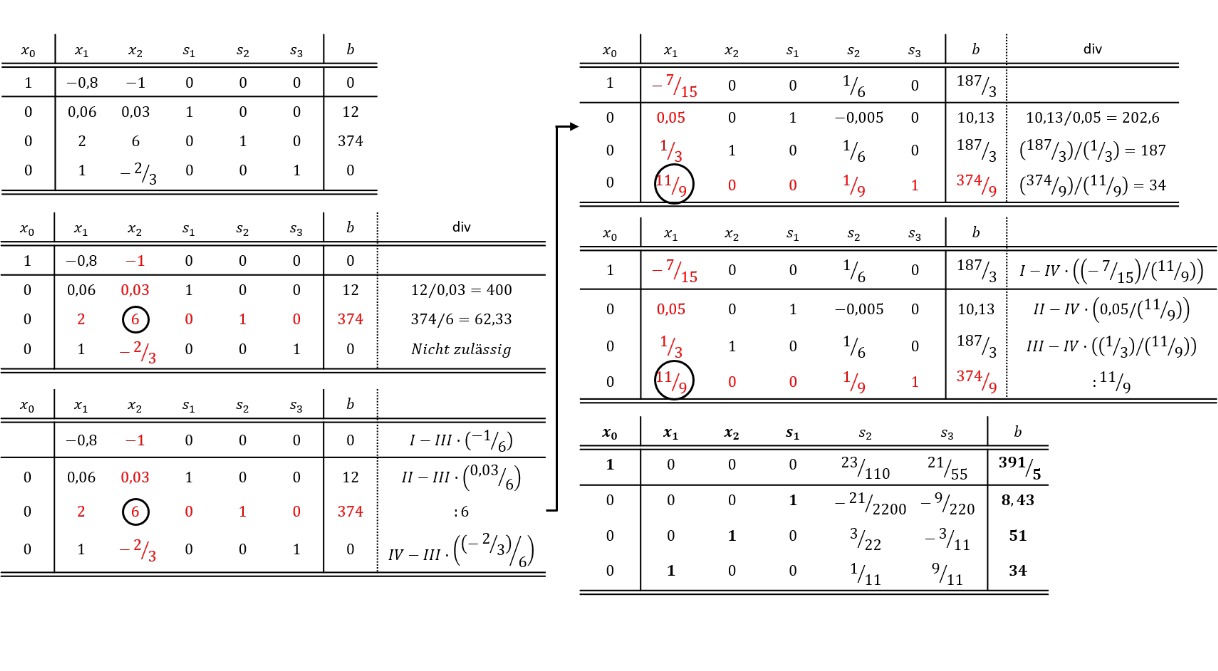
Beispielhafte Durchführung eines Pivot-Schritts:
Das allgemeine Prinzip der mathematischen Durchführung des Pivot-Schritts soll beispielhaft mit folgendem Simplextableau dargestellt werden:
Video "Simplex Verfahren":
Das Probe-Video behandelt die Thematik "Simplex Verfahren" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Ermittlung der optimalen Lösung eines Simplextableaus:
Mit dem Wissen, wie ein Pivot-Schritt durchgeführt wird, kann nun die optimale Lösung eines Simplextableaus ermittelt werden. Dazu gilt es so viele Pivot-Schritte nach demselben Ablauf durchzuführen, bis in der ersten Zeile (Zeile der Zielfunktion) kein negativer Wert mehr vorhanden ist. In diesem Fall gibt die Basislösung des Simplextableaus die optimale Lösung des linearen Optimierungsmodells an. Wir wollen die vollständige Ermittlung der optimalen Lösung mit folgendem gegebenen Simplextableau vollziehen, wobei wir Zwischenschritte zur Ermittlung des Pivotelements vornehmen werden:
Vertiefung Wirtschaftsmathematik-Paket
Übungen (optional)
20 h Lehrvideos
196 Skriptseiten
Formelsammlung
Klausurlösungen
Live-WebinareDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
