Zulässigkeitsbereich lineares Optimierungsproblem - Vertiefung der Wirtschaftsmathematik - Fernuni Hagen
Vertiefung Wirtschaftsmathematik-Paket > Vertiefung-Wirtschaftsmathematik > Lineare Optimierung
Allgemeine graphische Bestimmung von 𝒙_𝟏,𝒙_𝟐-Nebenbedingungen:
Die graphische Bestimmung des Zulässigkeitsbereichs erfolgt mittels den Nebenbedingungen des linearen Optimierungsmodells, wobei die Nichtnegativitätsbedingung das Koordinatensystem auf den positiven Bereich beschränkt. Um eine Nebenbedingung, die die Variablen 𝑥_1 und 𝑥_2 enthält, als Strecke in ein Koordinatensystem einzeichnen zu können, müssen die beiden Werte bestimmt werden, die die Nebenbedingung für 𝑥_1 bzw. 𝑥_2 annimmt, wenn für 𝑥_2 bzw. 𝑥_1 der Wert 0 gilt. Dadurch erhält man die beiden maximalen Werte der Nebenbedingung auf der 𝑥- bzw. 𝑦-Achse des Koordinatensystems, die sich zu einer begrenzenden Strecke verbinden lassen. Ob ein sofortiges Nullsetzen der einen Variablen und die Berechnung der anderen Variablen mit der unveränderten Nebenbedingung erfolgt, oder man zunächst mathematisch korrekt die Nebenbedingung nach 𝑥_2 umstellt und dann das Nullsetzen erfolgt, bleibt einem an und für sich selbst überlassen. Folgend sollen beide Vorgehensweisen und die Einzeichnung der Strecke anhand der folgenden Nebenbedingung darstellt werden:
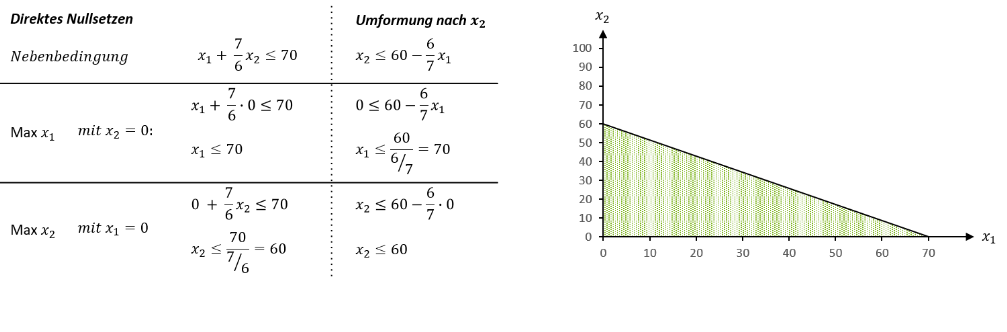
Allgemeine graphische Bestimmung von 𝒙_𝟏 oder 𝒙_𝟐-Nebenbedingungen:
Eine Nebenbedingung, die lediglich eine Variable 𝑥_1 oder 𝑥_2 begrenzt, kann direkt als Parallele zur 𝑦- bzw. zur 𝑥-Achse dargestellt werden, wie die folgenden Nebenbedingungen zeigen:
Video "Zulässigkeitsbereich lineares Optimierungsmodell":
Das Probe-Video behandelt die Thematik "Zulässigkeitsbereich lineares Optimierungsmodell" des Kurses "Vertiefung der Wirtschaftsmathematik" des Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Dieses Video ist ein Ausschnitt aus dem Inhalt des Vertiefung Wirtschaftsmathematik-Pakets.
Alle Thematiken des vollständigen Videos
Allgemeine graphische Bestimmung des Zulässigkeitsbereichs:
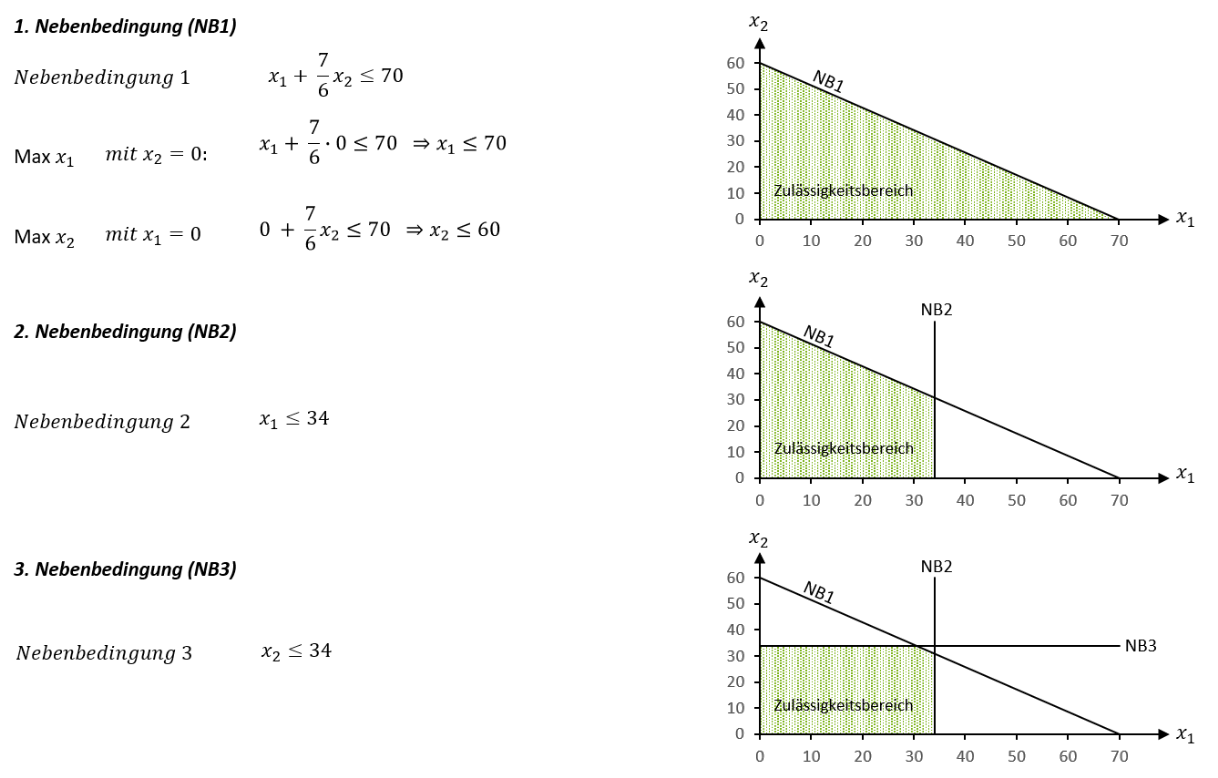
Zur graphischen Bestimmung des Zulässigkeitsbereichs sind alle sich ergebenden Strecken aus den Nebenbedingungen in eine einzelne Graphik gemeinsam einzuzeichnen. Der Zulässigkeitsbereich ist dann der Bereich, der vom Ursprung ausgehend keine der eingezeichneten Strecken aus den Nebenbedingungen überschreitet. Die Bestimmung des Zulässigkeitsbereich soll folgend anhand der uns bereits bekannten Nebenbedingungen schrittweise entwickelt werden:
Vertiefung Wirtschaftsmathematik-Paket
Klausurlösungen
Live-Webinare
Übungen (optional)
20 h Lehrvideos
196 Skriptseiten
FormelsammlungDas Vertiefung Wirtschaftsmathematik-Paket enthält den gesamten wirtschaftsmathematischen Teil des Kurses "Vertiefung der Linearen Algebra und Analysis" des Master-Moduls "Vertiefung der Wirtschaftsmathematik und Statistik" der Fernuni Hagen. Das Paket ist auf das erfolgreiche Bestehen der Klausur ausgerichtet. Der Aufbau folgt dem Kursskript der Fernuni Hagen und behandelt dabei alle wichtigen und klausurrelevanten Themen. Optional zum Paket stehen noch über 170 Übungsaufgaben, Übungsklausuren und zur Auffrischung wirtschaftsmathematischer Grundkenntnisse das "Grundlagen Wirtschaftsmathematik-Paket" zur Verfügung.
